コンデンサの合成容量の式の導出方法をわかりやすく解説

コンデンサの合成容量は以下の式で求められます。(Ct：合成容量)

$$並列接続の場合：C_{t}=C_{1}+C_{2}$$$$直列接続の場合：C_{t} = \frac{1}{{\frac{1}{C_1} + \frac{1}{C_2}}}$$

単に求めるだけなら式を覚えればOKです。しかしなぜこの式で求められるのかを理解し、導出ができると応用が効くようになります。すると試験に出てくる様々な問題に対応できるようになります。

そこでこのページでは合成容量の式を導出方法を詳しく解説していきます。

この先で解説しますが、まずはこの2点を覚えてください。これが合成容量を考える鍵になります。

ちなみにコンデンサの構造や静電容量の式がよく分からない方は、コチラ↓の記事を先に読むと理解がスムーズになります。

では解説に入っていきます。

並列接続されたコンデンサに掛かる電圧はなぜ等しい？

まず並列接続されたコンデンサにかかる電圧は図1のように等しくなることを押さえましょう。

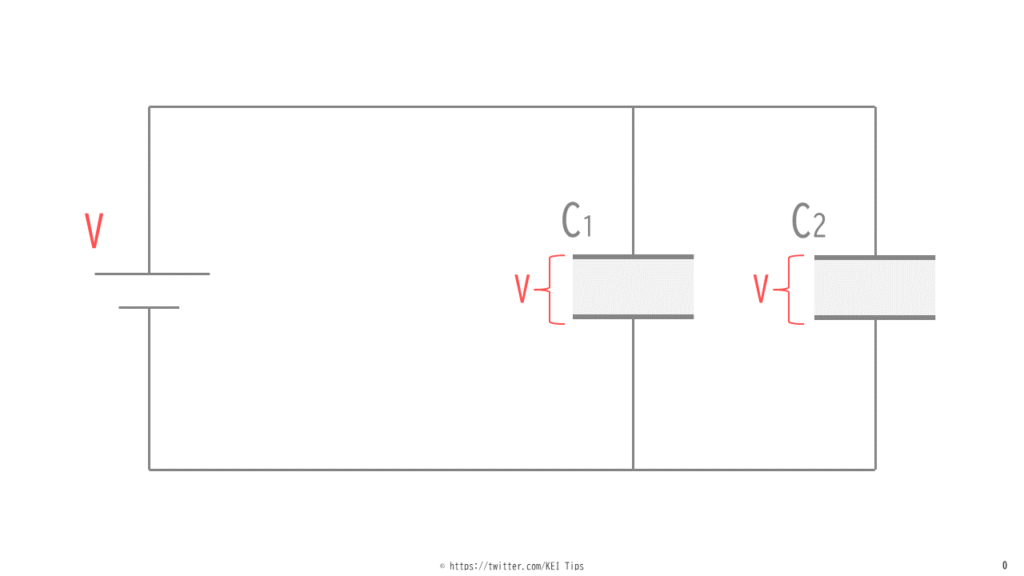
この理由は抵抗の並列回路と同じように考えればOKです。

並列に接続された抵抗は抵抗の大きさが同じでも異なっていてもかかる電圧は等しくなります。

コンデンサも同様に、静電容量が異なっていても並列に接続されていればかかる電圧は等しくなります。

並列接続されたコンデンサの合成容量の求め方

並列接続されたコンデンサの合成容量は各コンデンサの容量の和で求まります。なぜ和で求まるのかを導出していきましょう。

解説ではコンデンサの基本式である以下3つの式を使います。

$$Q=CV$$$$E=\frac{Q}{εS}$$$$V=Ed$$

$$Q:コンデンサに蓄えられた電荷、C:静電容量、V:極板間電圧、S:極板面積、E:極板間の電界の強さ、d:極板間距離$$

これが理解できていない方は、コチラ↓のページを先に読むと理解しやすくなります。

では図2のようにコンデンサが2つ並列接続されたケースを例に解説します。

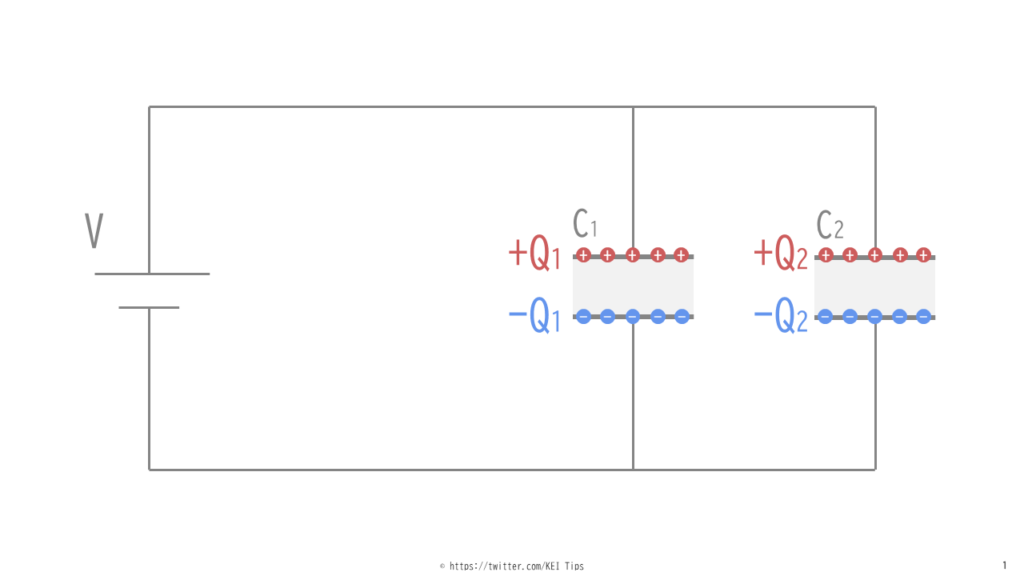
各コンデンサに貯まる電荷の合計をQ_tとします。(tはtotalの頭文字)

コンデンサの静電容量はそれぞれC₁、C₂として、貯まる電荷はQ₁、Q₂とします。すると

$$Q_{t}＝Q_{1}＋Q_{2}$$

になります。また、

$$Q_{1}=C_{1}V \quad Q_{2}=C_{2}V$$

です(電圧が同じなのでVが等しいため)。よって

$$Q_{t}＝C_{1}V＋C_{2}V$$

と求められます。この式の両辺をVで割ります。すると、

$$\frac{Q_{t}}{V}＝C1+C2$$

となります。ここでコンデンサの基本式であるQ=CVを思い出しましょう。

この式を少し変形すると、

$$\frac{Q_{t}}{V}＝C_{t}$$

です(C_tは合成容量)。先程求めた

$$\frac{Q_{t}}{V}=C_{1}+C_{2}$$

の式と一致します。よって、

$$C_{t}＝C_{1}+C_{2}$$

となります。このように並列接続されたコンデンサの合成容量は各コンデンサの容量の和であると導出できます。

直列接続されたコンデンサに貯まる電荷はなぜ等しい？

続いて直列接続されたコンデンサについてです。まずは直列接続されたコンデンサに貯まる電荷は等しくなることを理解しましょう。

これを図3で解説します。図3は2つのコンデンサが直列に接続され、直流電圧Vが印加されている様子です。

コンデンサC₁に貯まる電荷をQとすると、図4のようにC₁の上側の極板には+Qの電荷が蓄えられます。

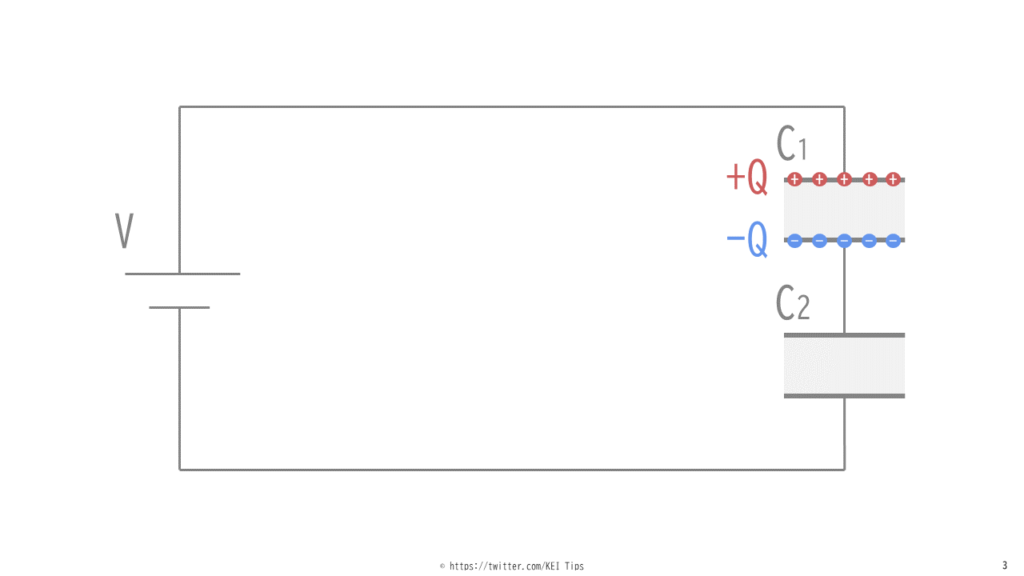
コンデンサの性質として一方の極板にプラスの電荷が蓄えられると、もう一方の極板には同じ量でマイナスの電荷が蓄えられます。

よってC₁の下側に貯まる電荷が－Qです。

次にC₂に貯まる電荷を考えます。C₁の下側の極板の電荷が－Qなので、図5のようにC₂の上側の極板には+Qの電荷が引き寄せられます。また上側の電荷が+Qなので、コンデンサの性質からC₂の下側の電荷は－Qになります。

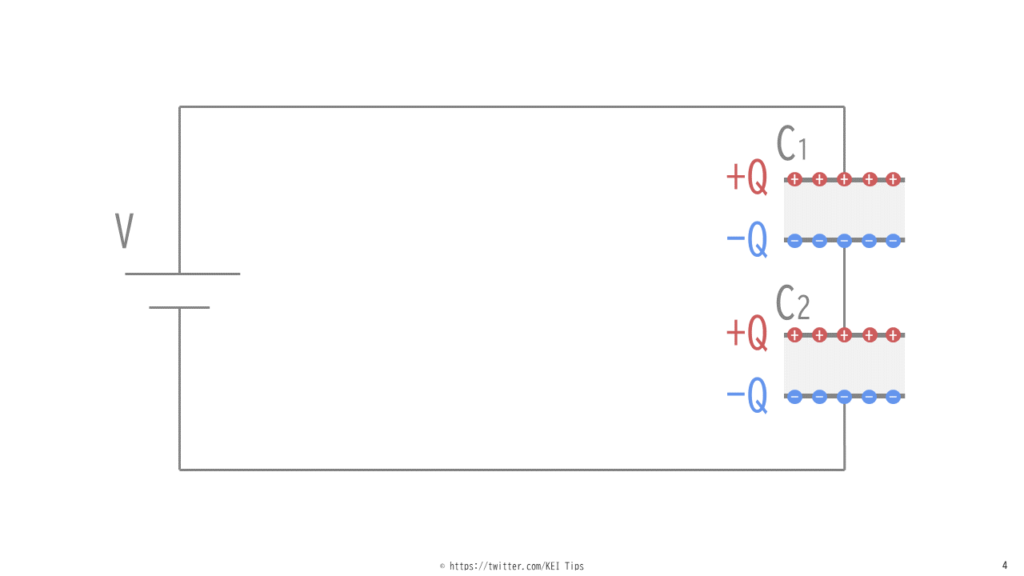
直列接続されたコンデンサが何個あっても、同様の考えで蓄えられる電荷は等しくなります。

直列接続されたコンデンサの合成容量の求め方

各コンデンサに蓄えられる電荷が等しいことを念頭に置いて、直列接続の場合の合成容量の式を導出していきます。

図6のように2つのコンデンサが直列の場合を例に考えましょう。

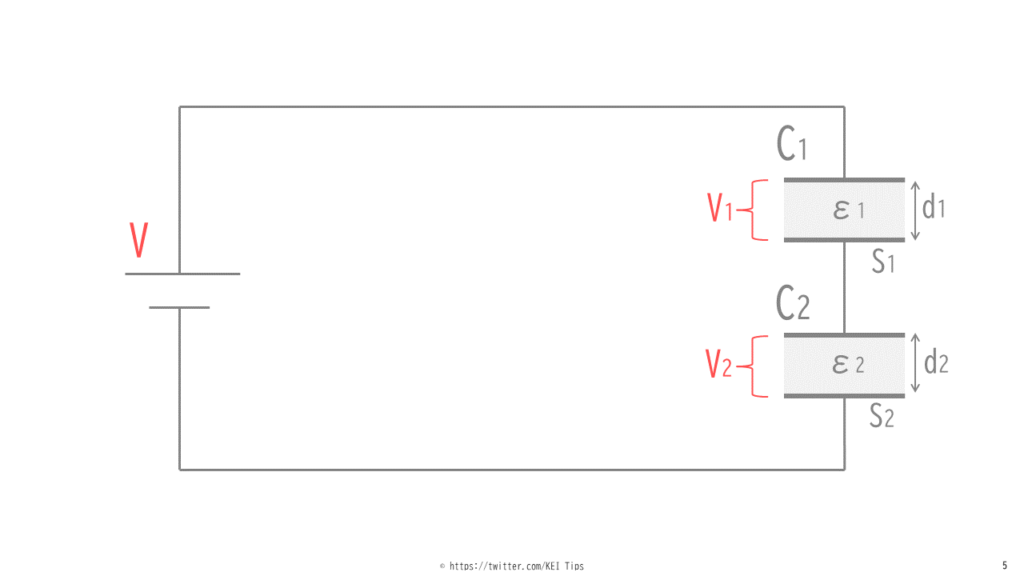
コンデンサC₁の電圧をV₁、C₂の電圧をV₂とすると、全体にかかる電圧V_tは

$$V_{t}=V_{1}+V_{2}$$

になります。ここでC₁とC₂の電界の強さをそれぞれE₁､E₂とします。蓄えられた電荷Qが等しいので、電界の強さはそれぞれ

$$E_{1}＝\frac{Q}{ε_{1}S_{1}} \quad E_{2}＝\frac{Q}{ε_{2}S_{2}}$$

と求められます。よってV=Edの式から電圧は

$$V_{1}＝E_{1}d_{1} \quad V_{2}＝E_{2}d_{2}$$

と求められます。全体の電圧V_t＝V₁+V₂ですので

$$V_{t}＝\frac{Q}{ε_{1}S_{1}}d1＋\frac{Q}{ε_{2}S_{2}}d2$$

となります。この式をQについて解く式に変形すると以下になります。

$$Q=\frac{1}{\frac{d_{1}}{\varepsilon_{1} S_{1}} + \frac{d_{2}}{\varepsilon_{2} S_{2}}}V_{t}$$

ここでコンデンサの基本式であるQ=CVをこの回路に適用すると、合成容量をC_tとすれば

$$Q=C_{t}V_{t}$$

です。先程求めた式と見比べると

$$C_{t}＝\frac{1}{\frac{d_{1}}{\varepsilon_{1} S_{1}} + \frac{d_{2}}{\varepsilon_{2} S_{2}}}$$

となります。C₁とC₂を使って表すと

$$C_{t}＝\frac{1}{\frac{1}{C_{1}}}+\frac{1}{\frac{1}{C_{2}}}$$

このように直列接続されたコンデンサの合成容量はこの記事の初めに記載した式になることを導出できます。