コンデンサの構造と役割、容量の求め方をわかりやすく解説

このページでは主に電験や電磁気学の勉強をする方に向けて、コンデンサの構造と役割、容量の求め方を分かりやすく解説します。コンデンサは式や数字だけで覚えていると理解も難しいですし応用問題に対応できません。

でも電荷がどのように移動するか？電気力線がどうなるか？について分かればすんなりと理解できます。コンデンサって難しいと思っている方はぜひ一読ください。

またYouTubeでもコンデンサの基礎について解説をしています。アニメーションで動きをつけて図解していますのでより分かりやすい内容になっています。ぜひこちらもご視聴ください。

コンデンサの構造

ではまずコンデンサの構造を把握しましょう。

コンデンサは2枚の金属板が向い合わせになっている

コンデンサは図1のように2枚の金属の板が向かい合わせになった構造をしています。

図では分かりやすくするため金属板の間のすきまを大きくしていますが実際はかなり狭い間隔です。金属板のことは極板と呼ばれることがほとんどです。ここからはコンデンサの金属板のことを極板と書くことにします。

極板の間は誘電体で満たされている

そして極板の間は誘電体で満たされています。

誘電体って何？という話はかなり難しいです。ここでは誘電体によってコンデンサが電気を蓄える能力が変わると覚えてもらえば十分です。

コンデンサの充電と電荷の移動

次にそもそもコンデンサの役割は？という話です。先に書いてしまいましたがコンデンサは電気を蓄える役割を持つ素子です。(素子は回路を構成する部品のこと。コイルや抵抗も素子です。)

ですから電圧をかけると充電します。これを図で確認しましょう。

コンデンサへ直流電圧をかけます。すると図3のように電荷がプラスとマイナスに分かれて極板へ移動していきます。

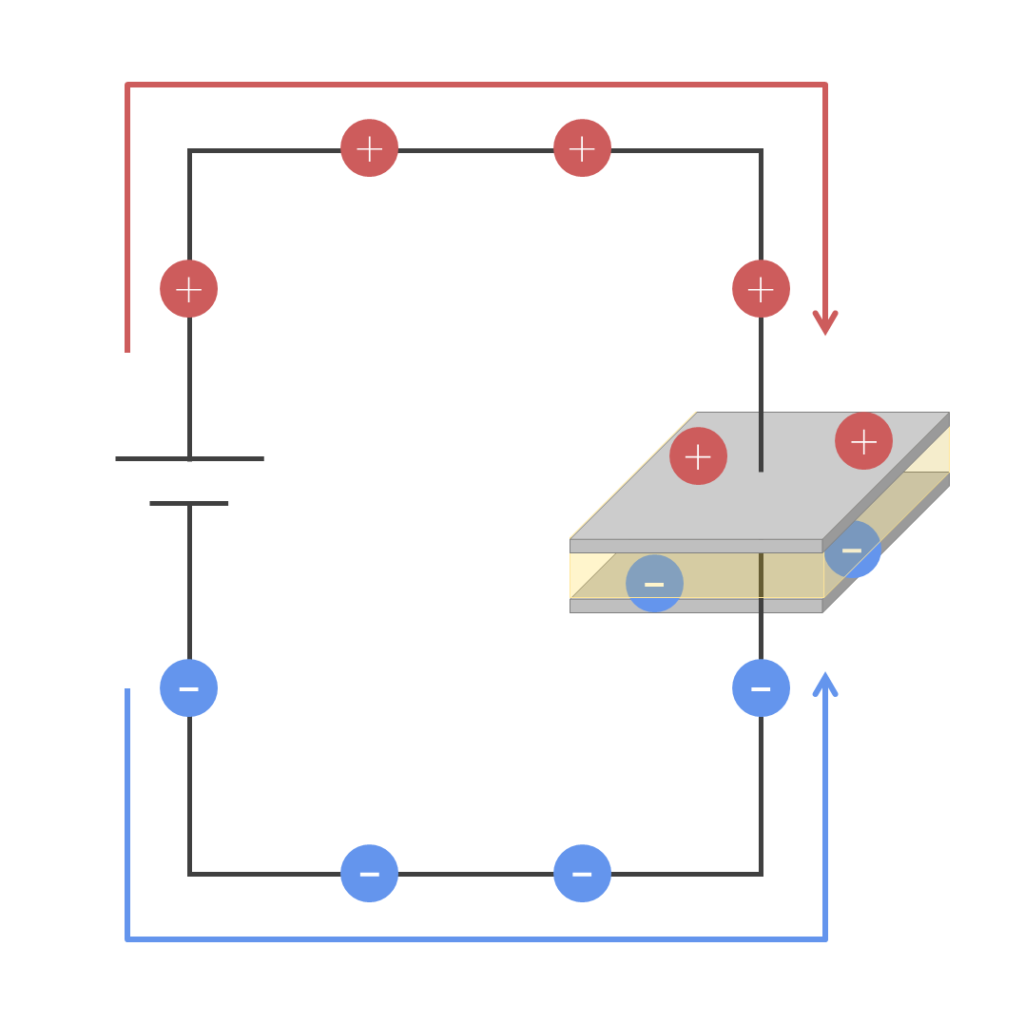
図4のように電荷の移動が無くなった状態を「充電された」といいます。

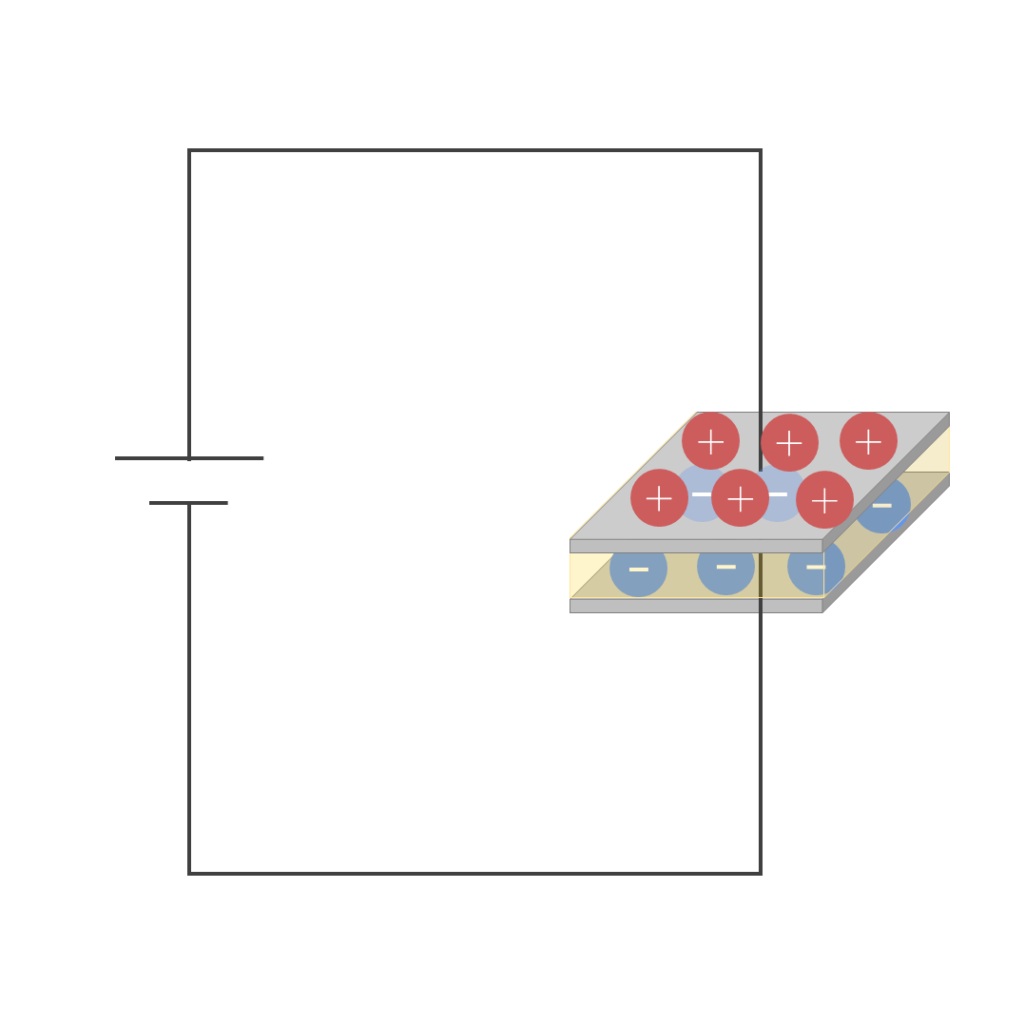
ここで理解してほしいポイントが極板に集まったプラスとマイナスの電荷は、クーロン力と呼ばれる力でお互いに引き寄せあっていることです。

詳しい説明は省きますが例えば下敷きで髪をこすると静電気でくっつきますよね？あれもクーロン力によるものです。

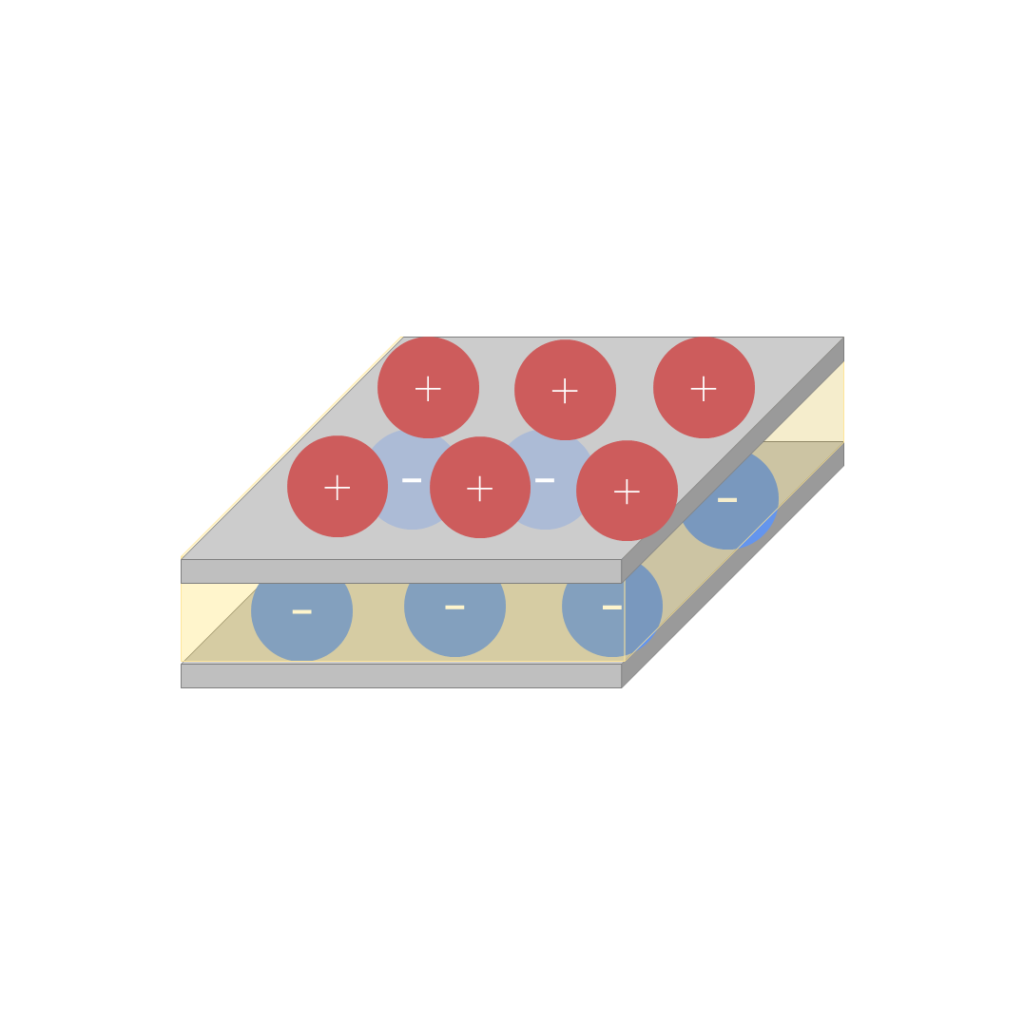
引き寄せあっているので、図5のようにコンデンサから電源を取っても電荷は極板に蓄えられたままになります。

コンデンサの静電容量

このようにコンデンサは電荷を蓄える素子ですが、コンデンサの能力によって蓄えられる電荷の量が変わります。このコンデンサの能力を静電容量といいます。

静電容量は次の式で求められます。(C:静電容量、S:極板の面積、d:極板間の距離、ε:誘電体の誘電率 図5参照)

$$C=ε\frac{S}{d}$$

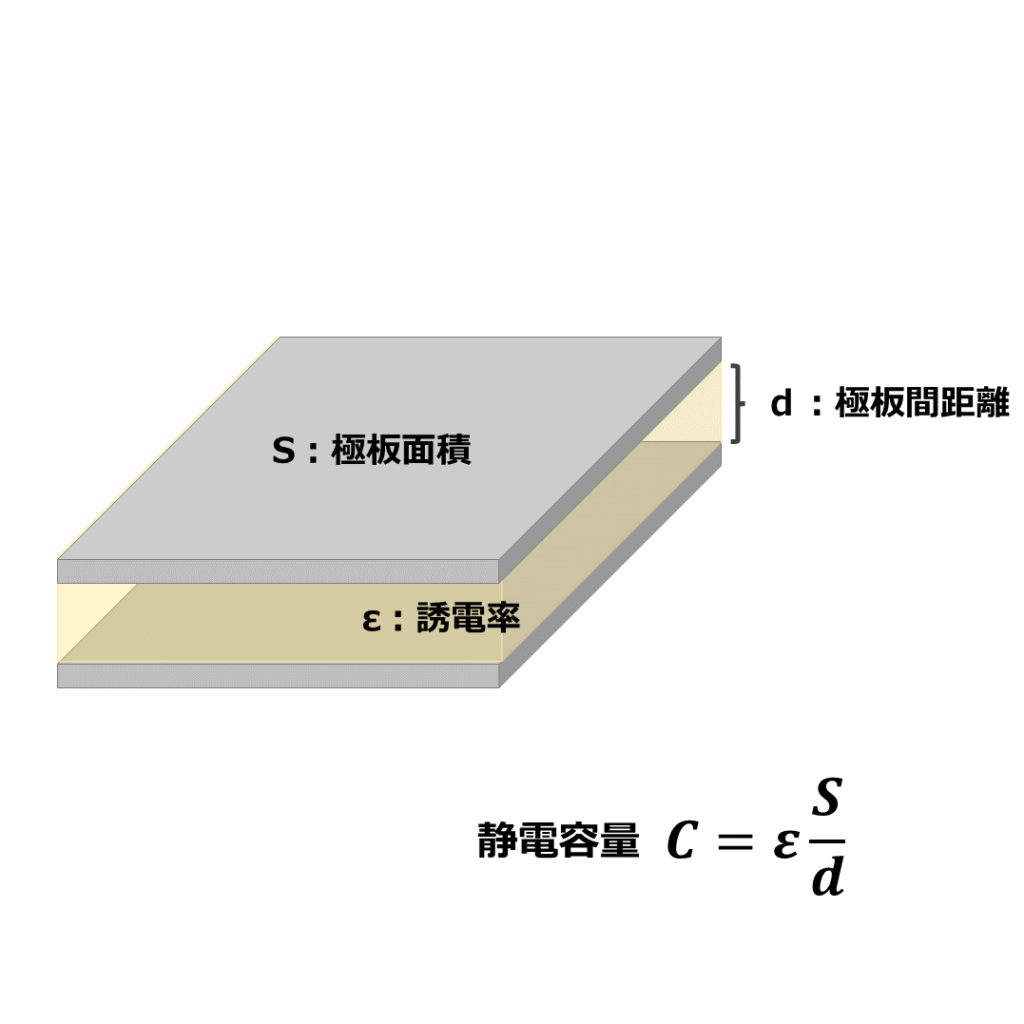
重要なのはこの式からコンデンサの構造によって静電容量が大きどう変化するかイメージすることです。この式からは次の3点が分かります。

コンデンサと電気力線

ここからは電荷が溜まったコンデンサの電解や電圧について理解するための解説です。まずは電気力線について理解するところから始めましょう。

電気力線とは電荷から出る力の線のこと

まず電気力線って何？って話です。電気力線は電荷から出る力の大きさや方向を矢印で表したものです。

コンデンサの電気力線はどうなる？

コンデンサでは極板に溜まった電荷から電気力線が出ます。

電気力線の特徴の一つが「プラスの電荷から出てマイナスの電荷に入る」ことです。そのため充電したコンデンサを真横から見た場合では図7のように電気力線が描けます。

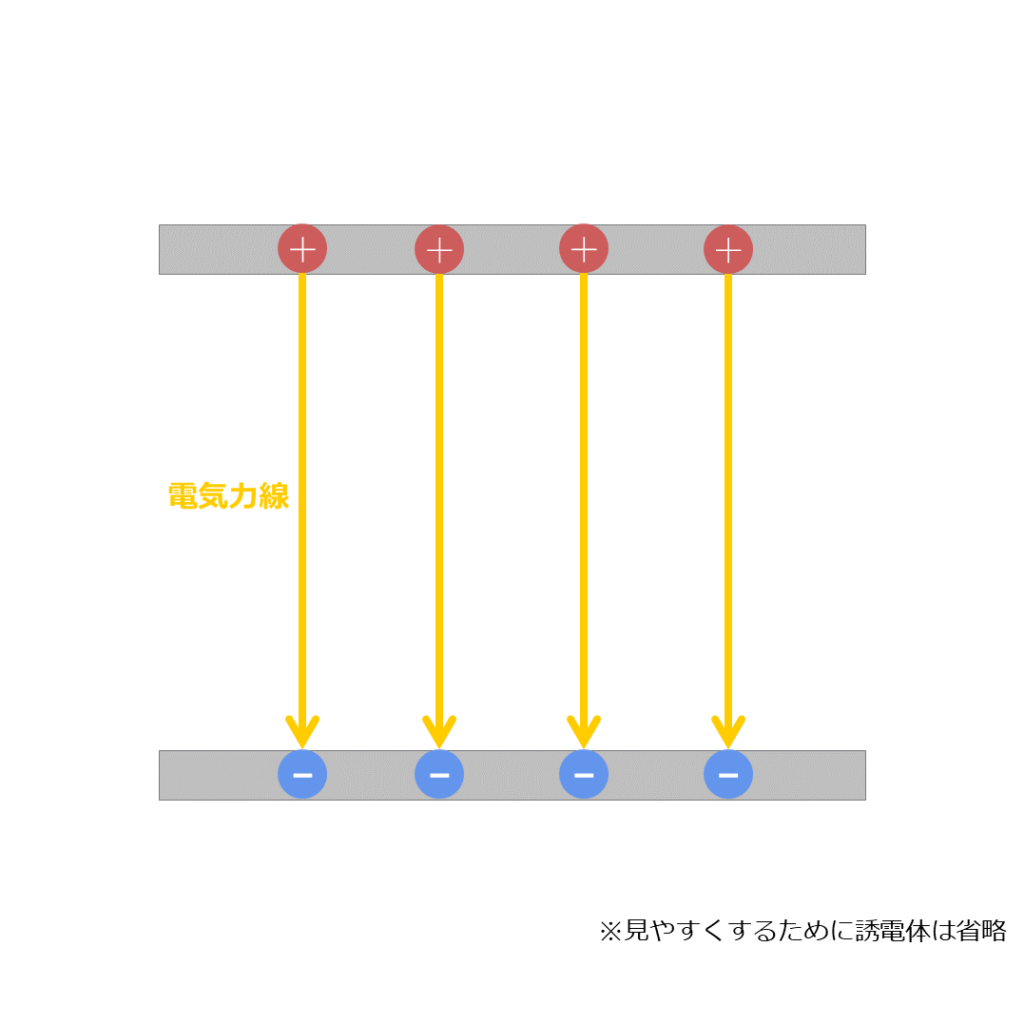
ここでのポイントは2つ。

これを理解しておきましょう。

コンデンサの極板間の電界の強さ

続いて電界の強さです。電界の強さは単位面積当たりの電気力線の本数で求められます。よって電気力線の本数を極板の面積で割ると求めることができます。式にすると以下です。

$$E＝\frac{Q}{εS}$$

コンデンサの極板間の電圧

コンデンサの極板間の電圧についても理解しましょう。

金属板の距離が広がると電圧も大きくなる

コンデンサの極板間の電圧を求める式はV＝Edです。つまり電界が強くなれば、または極板間の距離が広がると電圧も大きくなるということです。「電界が強くなれば電圧も大きい」これは何となく理解できますよね？

しかし「極板間が広がると電圧も大きくなる」ことはイメージがしにくいと思います。

そもそも電圧って何？これが分かると理解しやすい

これについてはそもそも電圧とは何か？が分かると理解できます。

電圧は電界中に置いた+1クーロンの電荷を移動させるのに必要な仕事(エネルギー)のことをいいます。コンデンサにおいては、マイナスに帯電した極板からプラスに帯電した極板まで+1Cの電荷を移動させたときのエネルギーが電圧になります。

分かりにくいですね。これも図で考えましょう。図8をみてください。

極板間を電気力線が通っています。ここに+1Cの電荷を置けばマイナスの極板の方へ動いていきます。ではマイナスの方へいったこの電荷をプラスの極板へ移動させるにはどうしますか？

外から別の力を加えるしかありませんね。実際にはできませんが例えとして電荷を指でつまんでプラスの方に移動させると考えてみましょう。

電荷にかかる力とは反対方向に動かすのでプラス側へ移動させるには指に力が必要です。仕事(エネルギー)はこの「力×距離」で求められます。そしてこの仕事は電圧のことでもありました。

コンデンサにおいては力は電荷にかかるクーロン力に等しくF＝QEで求められます。ここでは+1クーロンの電荷なので、掛かる力は電界の強さと同じです。

また距離は極板間距離と等しくなります。

そのため図9のように「極板間の電圧＝力×極板間距離」になります。

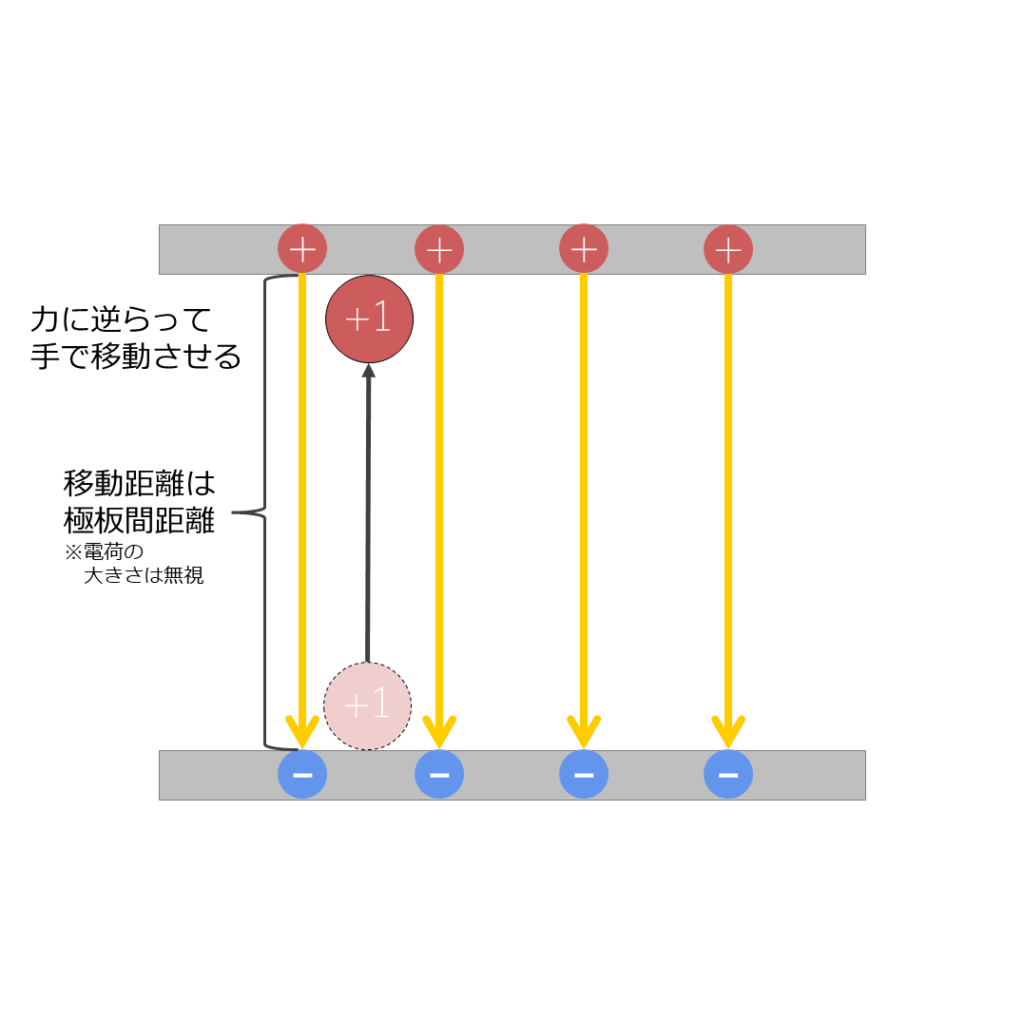
どうでしょう？極板間の距離が広がれば電圧も大きくなることが分かりましたね。

おわりに

以上を理解&イメージできればコンデンサの問題に苦労することが無くなるはずです。

本サイトではこのような解説を他にも行っています。もし質問や要望がありましたらお問い合わせかXのDMでご連絡いただければと思います。

またXの方でも電気理論の豆知識や簡単な解説を発信していますので、ぜひフォローをお願いいたします。