位相差とは？位相が遅れているか進んでいるかを見分ける方法を解説

交流回路の計算をするときに、まずつまづくのが位相のことだと思います。位相のことを理解できないと交流回路の計算はできません。

特に位相差とは何かを理解しておくことが大切です。

そこでこのページでは位相差や、併せてよく聞く遅れ・進みとはどういうことか？について解説します。

位相差を波形から理解する

まずは波形をみながら位相差について理解していきましょう。

位相差は基準となる波形との差

前提として位相差を考えるには基準となる波形が必要です。この波形とは交流の電圧や電流のことです。

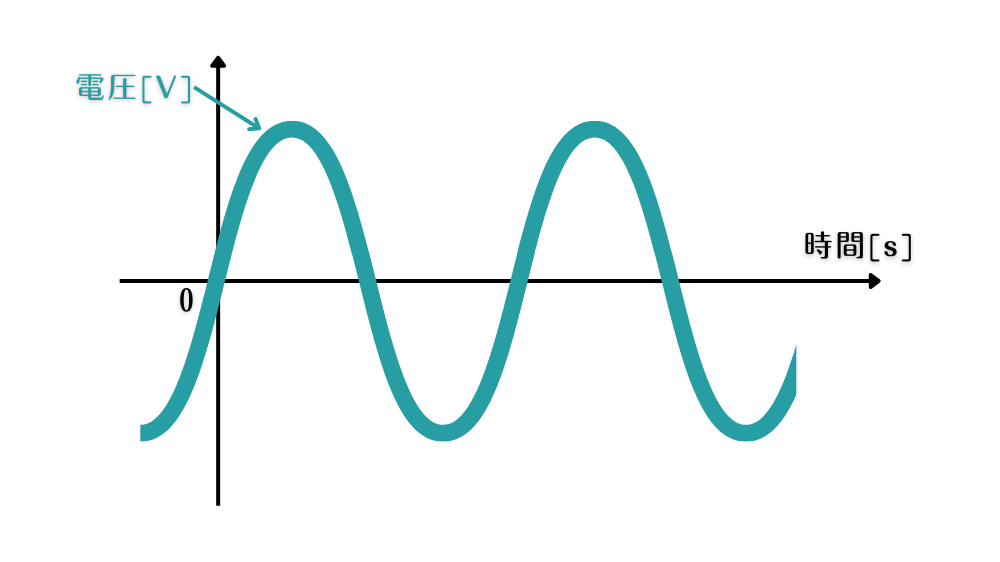
基準にする波形に決まりはないので、仮に図1のように0秒のときに0Vになる交流電圧を基準にして考えてみましょう。

基準より右側にくると遅れ

まずは遅れているとはどういうことかを解説します。遅れの波形として、図2のように電流波形を描きました。

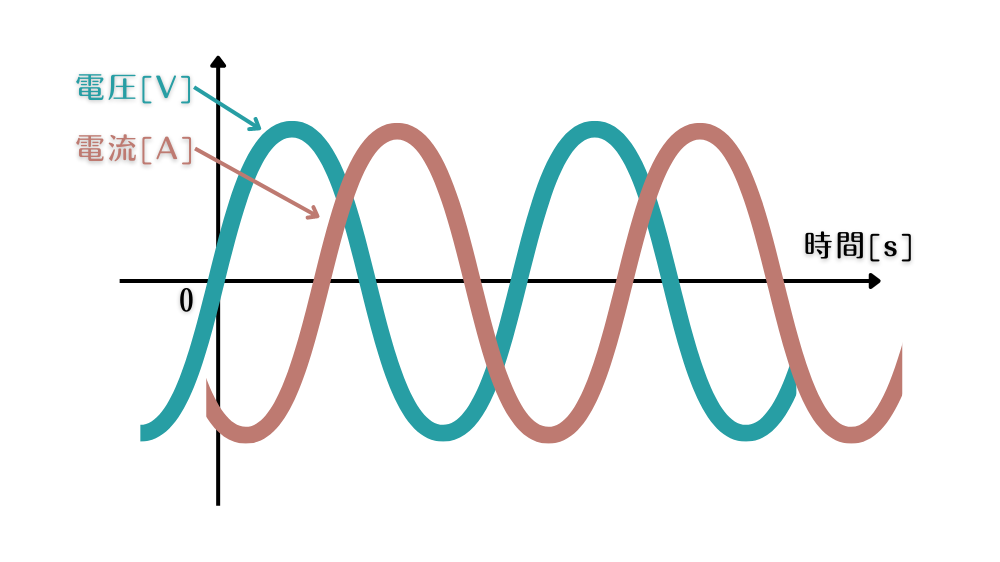
電流波形をみると基準である電圧波形より右側にあります。波形が基準より右側にあると、その波形は遅れているといいます。

この疑問はもっともです。右側にあれば遅れ。これは参考書にもよく書いてあるので、聞いたことがある人もいるんじゃないでしょうか？

でもなぜ右側だと遅れなんでしょうか？これが分からないと理解できないし覚えにくいですよね。

私が読んだある参考書には、そういうものだから覚えるしかないと書いてありました。でも私が思うにそれは間違っていると思います。そこで以下に書く考え方をすれば理屈が合うし覚えやすくなります。

波形が後から来るから遅れという

波形が基準より右にあるということは、基準より後からやってくる波形だということです。後からやって来るので遅れといいます。これを図で解説します。図3をみてください。

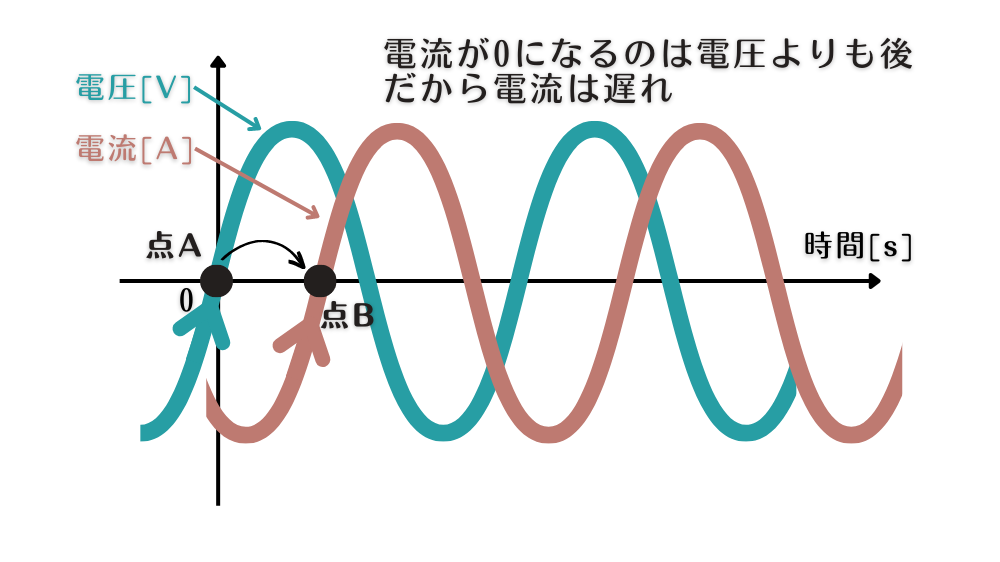
図の横軸は時間です。そして0秒を基準として左側が過去、右側が未来。こう考えてみます。

すると電圧は点Aのところで0Vになります。一方電流は少し右側の点Bで0になります。

つまり電圧が先に0Vになり、その後に電流が0になっています。よって電圧よりも電流が後からやって来たといえるのです。

このように基準に対し右側に波形があれば、基準よりあとからやって来たことになるので、その波形は遅れているといえます。

更に、波形が基準よりt秒右側にあればその波形はt秒遅れているといいます。

基準より左側にあれば進み

遅れが分かったところで、今度は進みの話です。といっても遅れとは反対に、左側にあれば進みと考えればOKです。

言い換えれば、基準より先にやってくるからその波形は進んでいるといえます。

この様に基準から何秒後の未来に(または何秒前の過去に)電流が来るか？を考えると位相の遅れ進みの判別は分かりやすくなります。

位相差を角度で表す方法

先ほどまでは位相差を時間[秒]で表していました。しかし電気の世界では位相を角度で表すのが普通です。そこで位相差を角度でどう表せばいいかを考えていきましょう。

また角度の単位は「度」が一般的ですが、電気の計算ではラジアンの方がよく使われます。
ラジアンも角度の単位で[rad]と書きます。ちなみに1rad=180/π[度]です。

ではt秒遅れている場合、何ラジアン遅れていることになるでしょうか？ということを考えていきます。

まずは角周波数を求める

位相差を角度で表現する場合は、まず角周波数ω[rad/s]を求めます。角周波数は次の式で求められます。

ω＝2πf　※おめがイコール2パイエフを連呼して覚えましょう。

角周波数に時間をかける

そしてこの角周波数ωに時間[秒]をかけると角度が求められます。

つまりt秒遅れなら、角度＝ωt[rad]です。

よってωt[rad]位相が遅れていると求めることができます。

おわりに

本サイトでは電気に関してこのような初学者でも分かりやすい解説を行っています。

またXの方でも電気理論の豆知識や簡単な解説を発信していますので、ぜひフォローをお願いいたします。