位相差の求め方と位相差を角度で表す方法

電験の交流回路の問題では、問題を解くために位相差を求める場面がよくあります。ここでは位相差の求め方について解説をします。

位相差とは？

まずは位相差が何かについておさらいしましょう。位相差とは2つの波が時間的にどれくらいずれているかを表します。
図1は位相がずれた2つの波形です。図1で示した時間的なずれのことを位相差といいます。

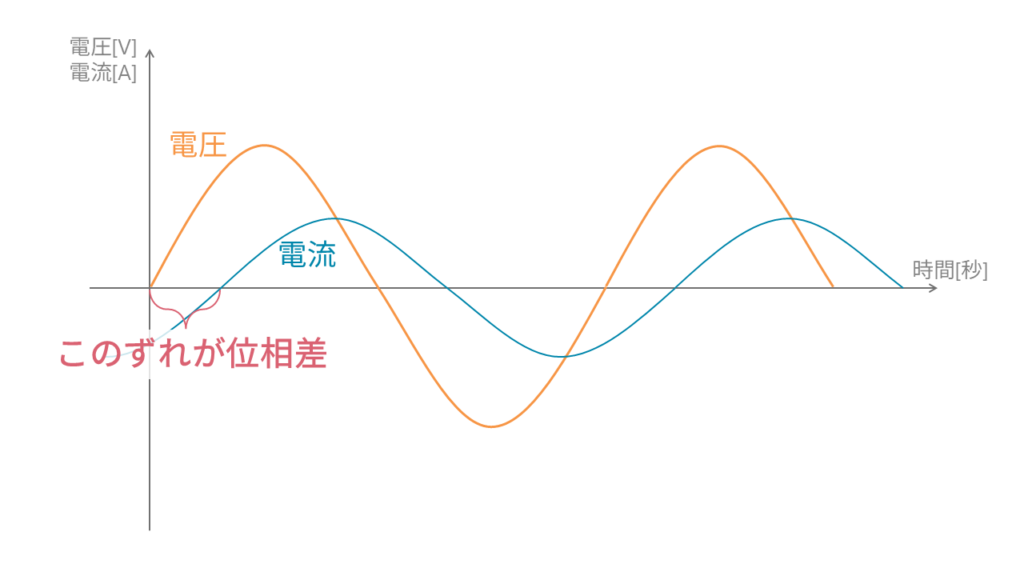
位相差の求め方

位相差は時間的なずれのことですが、角度で表すことがほとんどです。
時間を角度で表す？と聞くと難しそうですが、交流回路を考えるうえで非常に重要ですので、じっくりと理解していきましょう。

360°で1周期と考える

時間を角度で表すためには、1周期を360°として考える必要があります。これは図で考えたほうが早いです。図2をみてください。

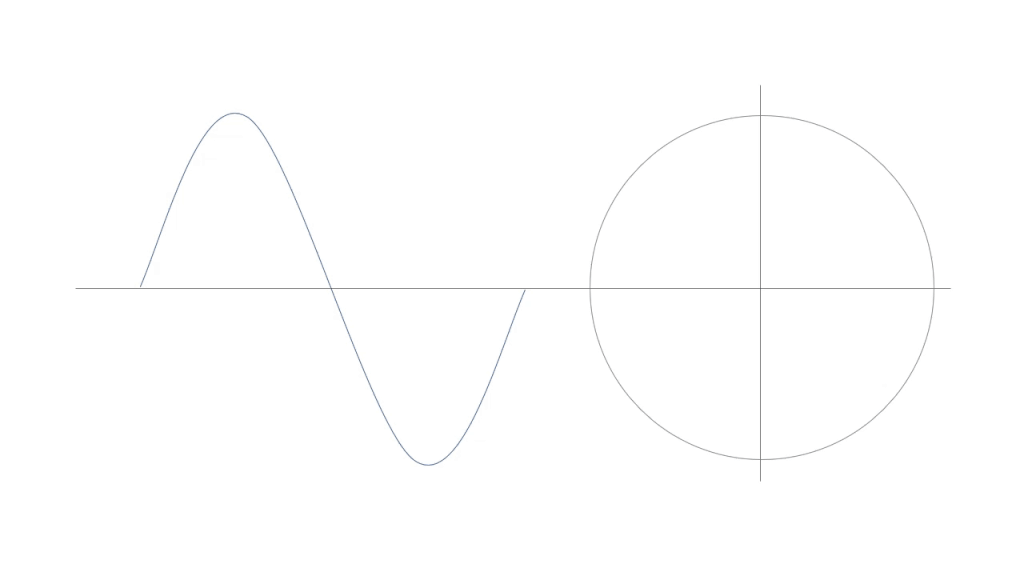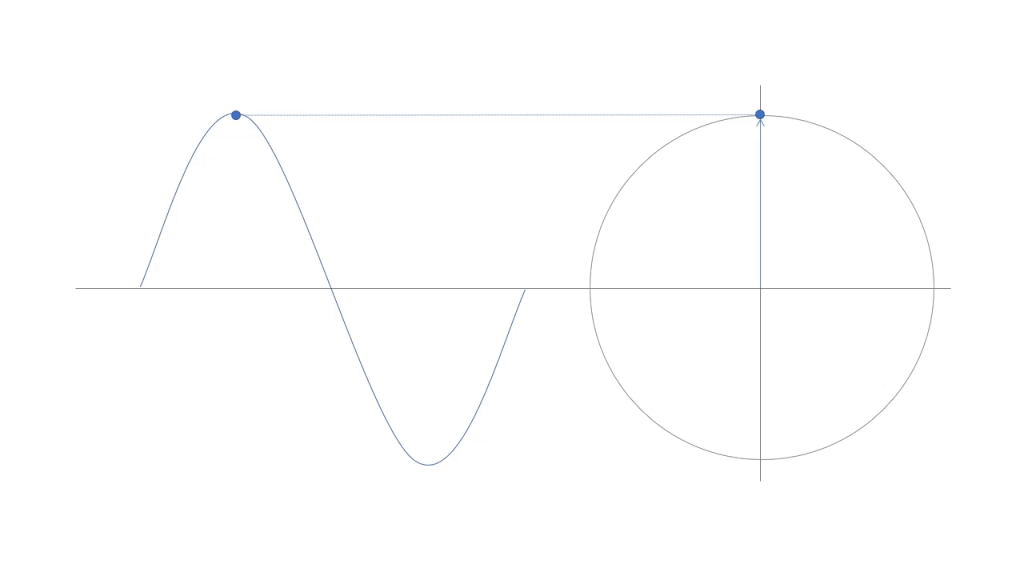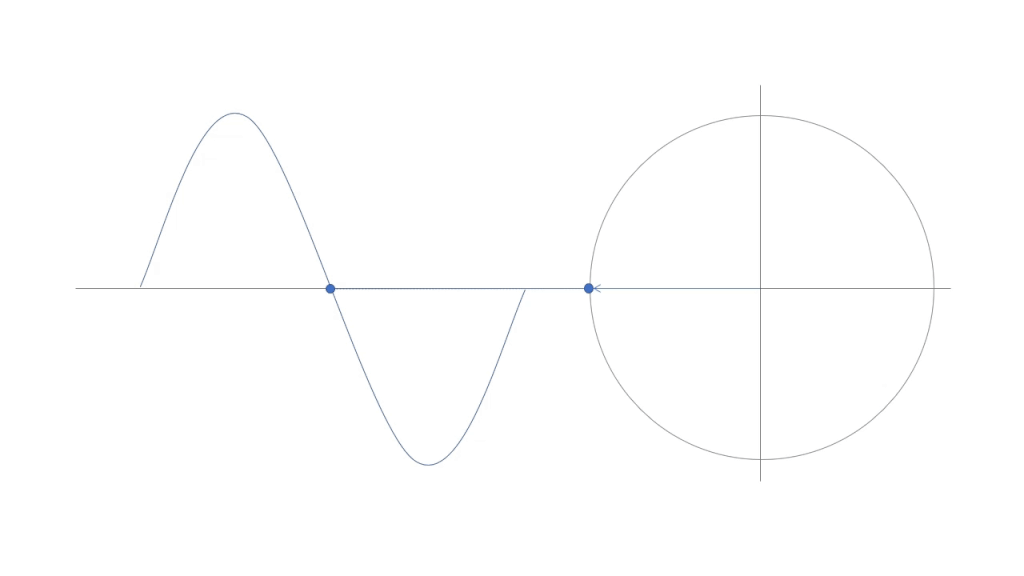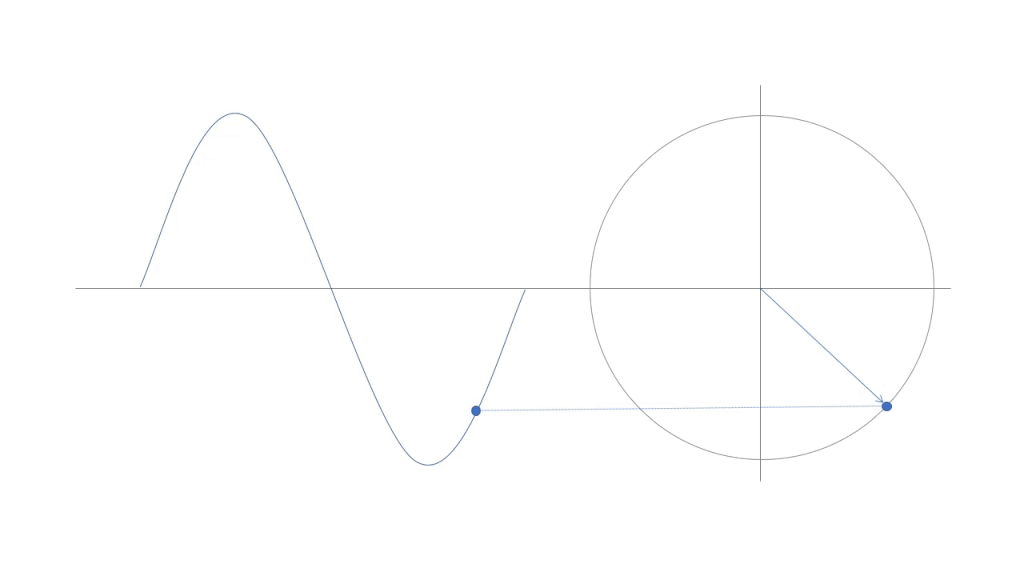
図2のように、周期的な波形は1周期を360°として考えることができます。波が1/4周期進んむと90°、1/2周期なら180°、3/4周期なら270°となります。
また波が1周期進んだら、360°となり元の位置に戻ります。

周期的な波は同じ動きを繰り返します。また角度は円運動ですから同じ動きを繰り返します。だから波の進んだ時間を角度として表すことができます。まずはこのイメージを持ってください。

位相差を角度で表す

時間が角度で表せることがわかったところで、位相差を角度に変換する具体的な方法を解説します。
これには以下の式を使います。

$$位相差[°]=360°\times\frac{位相差[秒]}{周期[秒]}$$

この式は360°のうち、波が何割進んだかを求めています。このようにして位相差は角度として表すことができます。

角度をラジアンで表す

以上では角度の単位は°(度)で求めました。しかし電気の計算では角度の単位はラジアンを使うことがほとんどです。
そのため°(度)をラジアンに変換してみましょう。°(度)とラジアンには以下の関係性があります。

$$360°=2πラジアン$$

ちなみにラジアンはアルファベットで[rad]と書きます。以下からは[rad]で表記していきます。
この式を1°＝〇〇の形に直すと、

$$1°=\frac{π}{180}[rad]$$

となります。例えば180°をradに直すには、この式の両辺に180を掛ければOKです。つまり以下の式が°(度)をradに変換する式になります。

$$角度[rad]=角度[°]\times\frac{π}{180}$$

2つの波形の周波数が違うと位相差の求め方も変わる

以上の解説を読んで勘の良い方はお気づきかもしれません。2つの波形の周波数が異なる場合は位相差の求め方はもっと複雑になります。

しかし電験3種ではあまり考えなくても良いでしょう。なぜなら電験3種の交流回路の問題で出てくる波形は、商用周波数の電圧、電流だからです。
商用周波数とは50Hzもしくは60Hzの、日本の電力で使われる周波数のことです。
実務上でもこれ以外の周波数を扱うことはあまりありませんので、気にすることはないです。