科学関係の計算は3.15767324・・・・
のように小数がたくさん出たり、割り切れない値が出てくることが多いです。
ここで悩むのが「どこで四捨五入をすれば良いんだ？」ということではないでしょうか？
この疑問は有効数字を正しく理解することで解消します。なぜなら計算に使う値は通常は有効数字だからです。
ここでは以下2点について細かいルールを省き、根本的な考え方にフォーカスした解説をします。
- 有効数字とは何か
- 計算をする際にどこで四捨五入をすれば良いか？
有効数字とは？
有効数字の意味
有効数字とは測定誤差を含んだ値のことを指します。
どういう意味か図解します。
図1はある物体の長さを定規で測っている様子です。定規の大メモリは1m、小メモリは0.1mです。科学ではメモリが無い部分まで、目視で読み取った値を測定値にする決まりがあります。
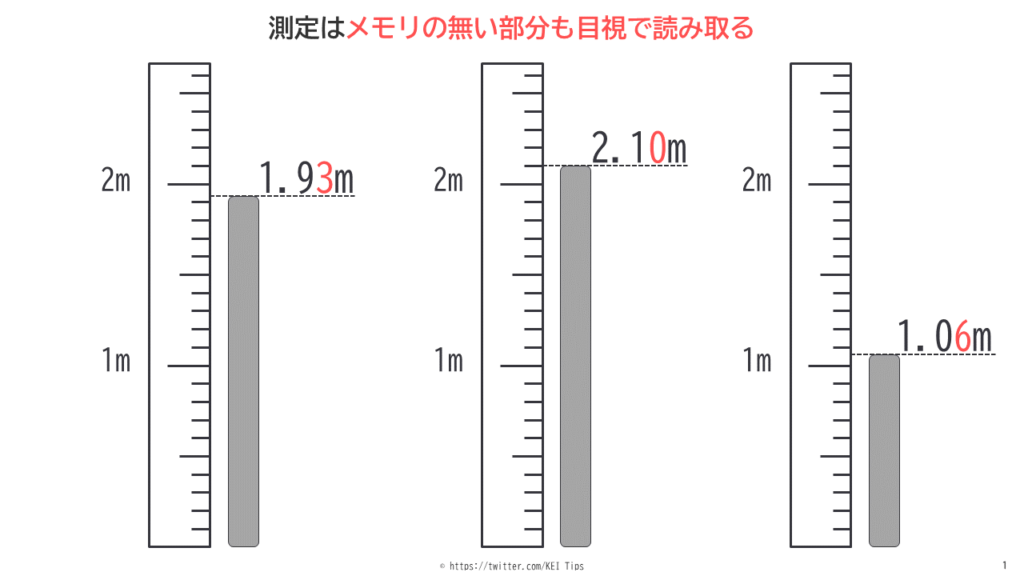
しかし目視で読み取った値は、極端にいえば人が勘で読み取った値なので誤差があります。
有効数字はこの誤差を含んだ値ということです。例えば有効数字3桁なら図2のように3桁目は誤差があることを意味します。
前述したように科学の世界ではこの誤差を含んだ値までを測定値とするのがルールです。
有効数字の末尾の0は消してはいけない
では有効数字についてもう一つ重要な点を解説します。例えば先程の図の有効数字3桁で2.10という数字で、
末尾の0は消して2.2としても良いのでしょうか？
結論から言うとダメです。理由はこの0の有無で数値の意味が大きく変わるからです。
有効数字3桁なら3桁目に誤差があると前項で説明しました。この誤差がどれくらいかというと2.20は2.195～2.205の間の値になります。(正確には2.195以上、2.205未満)
末尾の0を消した2.2でも同様に考えると・・・
2.2は2.15～2.25の間の値です。
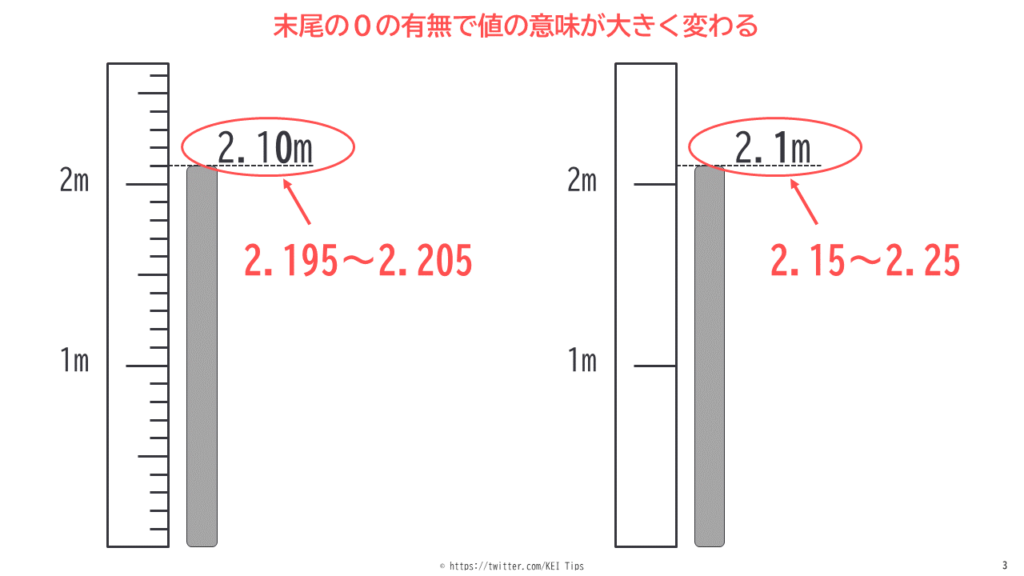
このように末尾の0を消してしまうと違う値になってしまうので、ちょっと0を忘れただけは通用しません。
有効数字の計算について
では有効数字が分かったところで、計算はどのようにすれば良いかを解説します。
有効数字同士の計算値の下位の数字は意味が無い
有効数字の計算をする上でのポイントは下位の数字は意味が無い数ということです。
例えばどちらも有効数字3桁として1.93×1.06を筆算で求めてみましょうすると以下3つのタイプの値に分かれます。
×誤差がある値同士の計算値
△誤差がある値と無い値の計算値
〇誤差が無い値同士の計算値
それぞれに×△〇をつけると図4の左側のようになります。
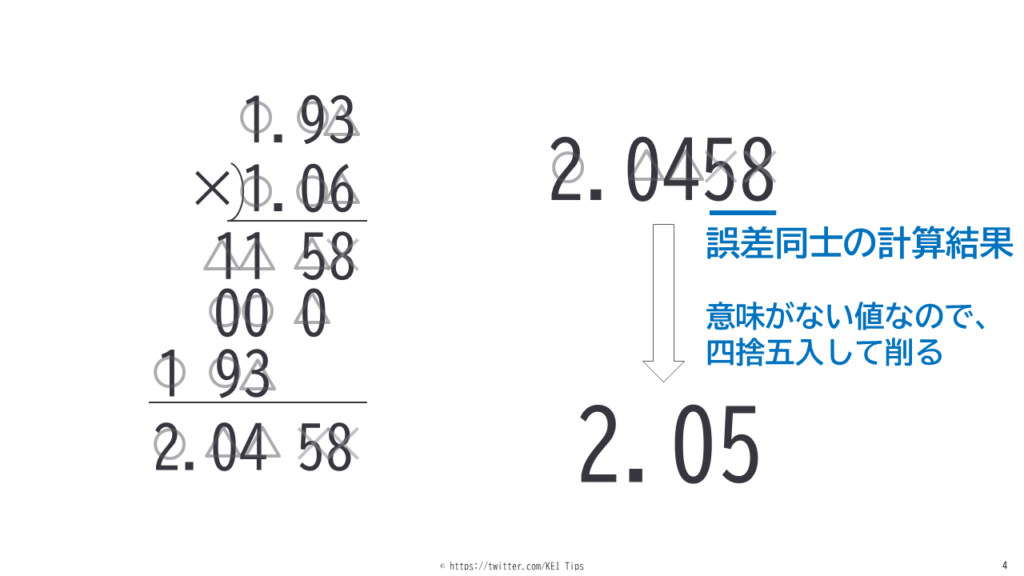
ここで計算結果にも✕△◯をつけると以下のように考えることができます。
×は誤差だらけで意味が無い値
△は多少誤差があるが許容範囲な値
〇は誤差が無い値
そのため計算結果からは意味のない×の値を消す必要があります。よって図4の右側のように四捨五入をします。
これが有効数字の計算の根っこの考え方です。
有効数字は一番小さい桁に合わせる
根本的な理解ができたので、今度は実際に計算するときはどうしたら良いか？を解説します。
まず有効数字〇桁で求めよという指定があればこれに従って計算をするだけです。
一方で指定がない場合は、与えられた値のなかで一番有効数字の桁が小さい値に合わせます。
例えば有効数字3桁の1.93と2桁の2.1の掛け算を求めるなら、計算結果の有効数字は2桁にします。
四捨五入をするタイミングは？
さきほどは2つの値の計算だったので、最後の計算結果を四捨五入すればOKでした。
しかし普通は一つ計算結果がでたら、それにまた別の値をかけたり割ったりすることが多いです。
この場合は四捨五入をどこですれば良いかを解説します。
では1.93×2.14の計算結果に3.27をかけるケースを例に説明します。ここでは最終的な値を有効数字3桁で求めるとします。
まず1.93×2.14＝4.1302
最終的な結果を有効数字◯桁で求める指定がある場合は、計算で使う桁を◯＋1桁として計算を進めるルールがあります。
よって1.93×2.14＝4.1302=4.130
この計算結果に更に3.27をかけます。
4.130×3.27＝13.5051
ここで指定された有効数字3桁にするために、四捨五入をします。
4.130×3.27＝13.5051=13.5
答え13.5
計算中は指定の有効数字より1桁多くとって計算を進めていく。そして最終的な計算結果を四捨五入して指定の桁にあわせる。
これが有効数字で計算するときの四捨五入のタイミングになります。
おわりに
本サイトでは電気に関してこのような初学者でも分かりやすい解説を行っています。
もしこれを解説してほしい！という要望や質問がありましたらお問い合わせかXのDMでご連絡いただければと思います。
コメント