ΔY変換とは？
三相負荷は図1のようにΔ結線とY結線があります。
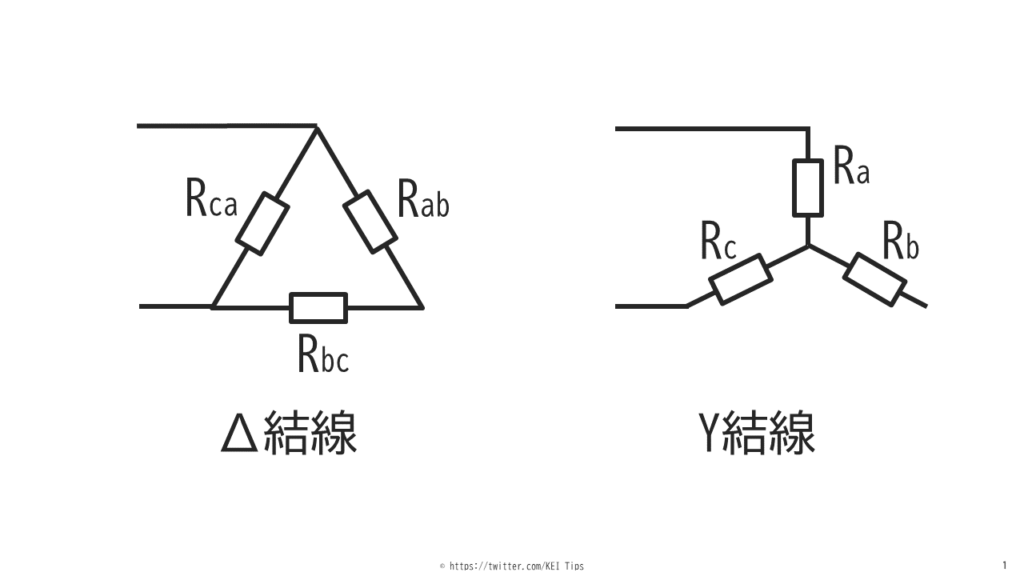
Δ結線の負荷をY結線に換算したら抵抗値はどうなるか？
逆にY結線の負荷をΔ結線に換算したときの抵抗値は？
これらを知りたいときは以下の計算で求められます。
Δ結線からY結線に換算する場合
$$R_a=\frac{R_{ab}R_{ca}}{R_{ab}+R_{bc}+R_{ca}}$$
$$R_b=\frac{R_{ab}R_{bc}}{R_{ab}+R_{bc}+R_{ca}}$$
$$R_c=\frac{R_{bc}R_{ca}}{R_{ab}+R_{bc}+R_{ca}}$$
Y結線からΔ結線に換算する場合
$$R_{ab}=\frac{R_aR_b+R_bR_c+R_cR_a}{R_c}$$
$$R_{bc}=\frac{R_aR_b+R_bR_c+R_cR_a}{R_a}$$
$$R_{ca}=\frac{R_aR_b+R_bR_c+R_cR_a}{R_a}$$
この計算をΔY変換(YΔ変換)といいます。
なぜΔY変換の式で抵抗値が求まるのか？
ここでなぜΔY変換の式で負荷の抵抗値を換算できるのか？という疑問が出るかと思います。
これは「なぜ？」というよりは計算で辻褄が合うように調整している。と考えた方が分かりやすいです。
どういうことか以下で詳しく解説します。
Δ→Y(Y→Δ)変換の理屈
ΔからY(またはYからΔ)結線に負荷の抵抗値を変換する理屈を理解するには図2のように↓がポイントになります。
「ΔからY(またはYからΔ)へ結線を変えても2線間の合成抵抗値は同じ」
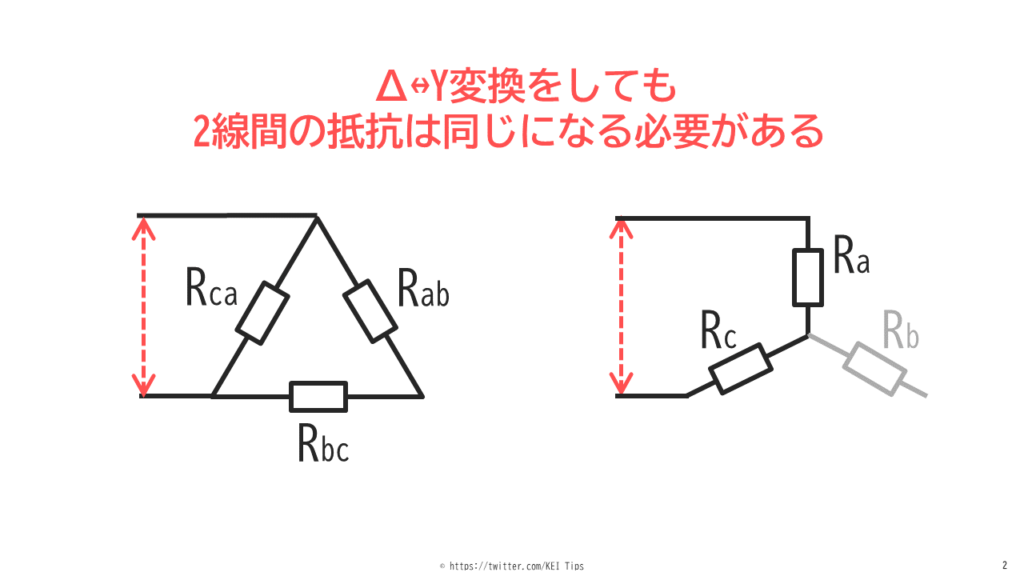
この理由はΔからYへ変換しても、この2つは回路的に同じだからです。
ではΔ→Y変換をしても2線間の合成抵抗値は同じということを念頭において解説を進めます。
2線間の合成抵抗値は同じであるので、図3で示す線間の合成抵抗値RΔ2とRY2が等しくなります。
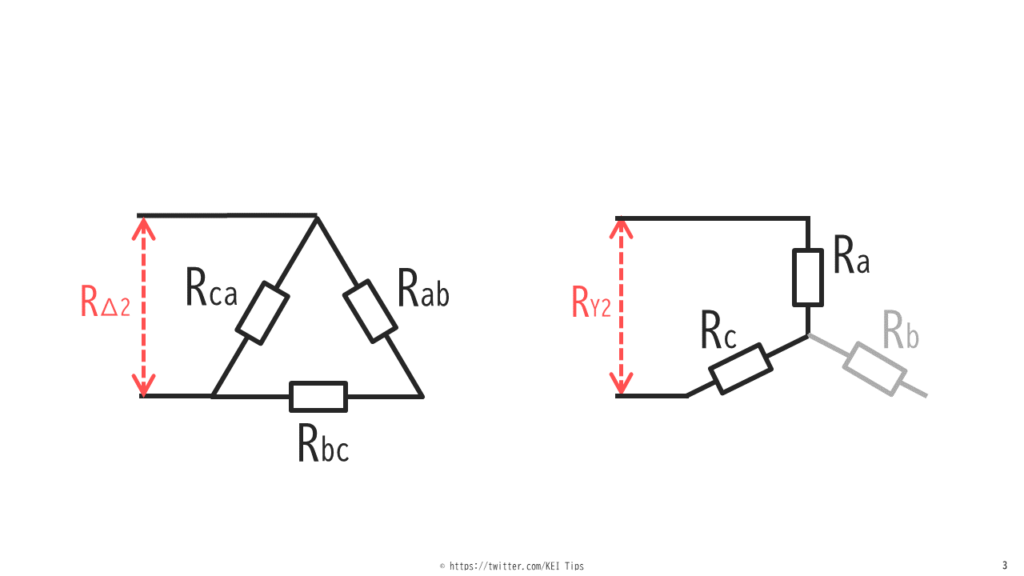
図3から2線間の抵抗を抜き出して見やすくすると図4になります。
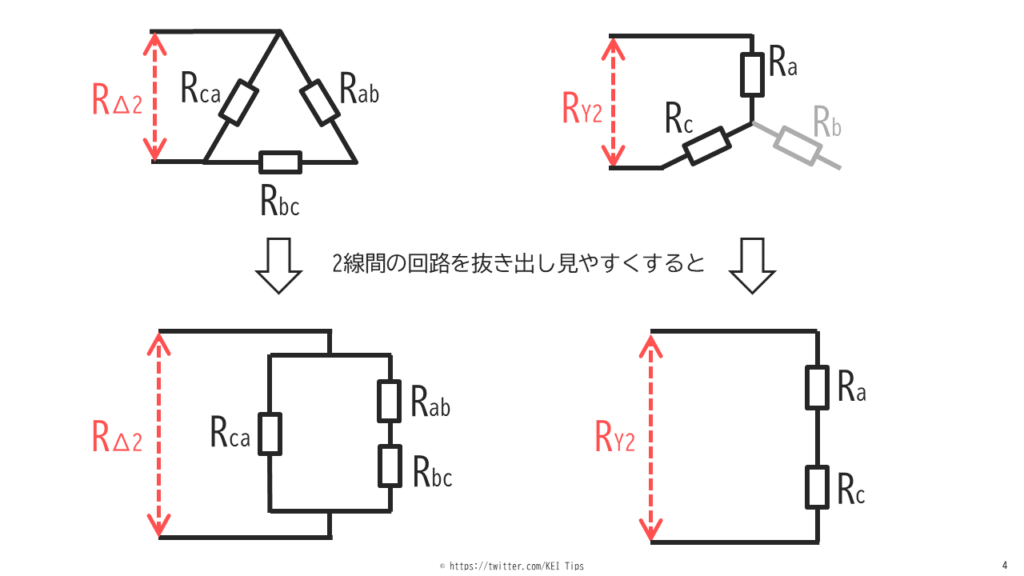
合成抵抗RΔとRYをそれぞれ計算すると以下になります。
$$R_{Δ2}=\frac{R_{ca}(R_{ab}+R_{bc})}{R_{ca}+(R_{ab}+R_{bc})}$$
$$R_{Y2}=R_a+R_c$$
2線間の合成抵抗値は同じなのでRΔ2＝RY2です。
三相平衡負荷の場合で考える
ここで回路が三相平衡負荷の場合で考えてみましょう。
三相平衡負荷とは各相の負荷の抵抗値が等しいということです。
よって図5のようになります。
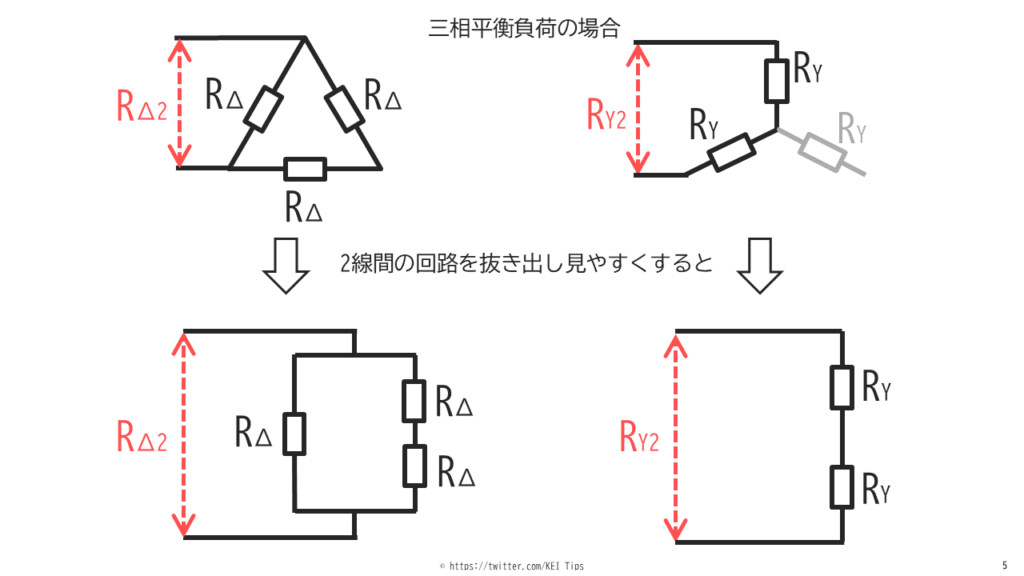
先ほど求めた式RΔ2とRY2に各抵抗値を当てはめてみましょう。すると↓のようになります。
$$R_{Δ2}=\frac{R_Δ(R_Δ+R_Δ)}{R_Δ+(R_Δ+R_Δ)}=\frac{2}{3}R_Δ$$
$$R_{Y2}=R_Y+R_Y=2R_Y$$
RΔ2＝RY2なので
$$\frac{2}{3}R_Δ=2R_Y$$
つまり
$$R_Δ=3R_Y$$
これはつまり図6のようにΔ→Y結線に変換すると抵抗値は1/3倍、Y→Δ結線に変換すると抵抗値は3倍になることを表します。
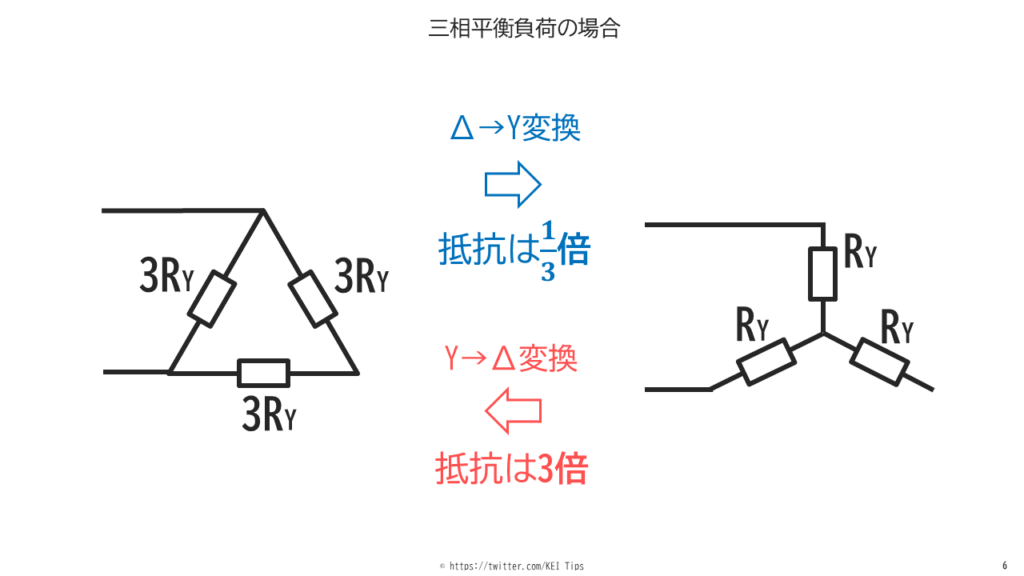
参考書などでは平衡負荷なら上記のように3倍、1/3倍になるといった説明がされています。この理屈はこういうことです。
三相不平衡負荷の場合は？
では三相平衡負荷の場合でも考えてみましょう。
三相不平衡負荷とは各相の抵抗値が異なる負荷のことです。
この場合もポイントは同じで2線間の合成抵抗値が等しいということから、図7のように式が立てられます。
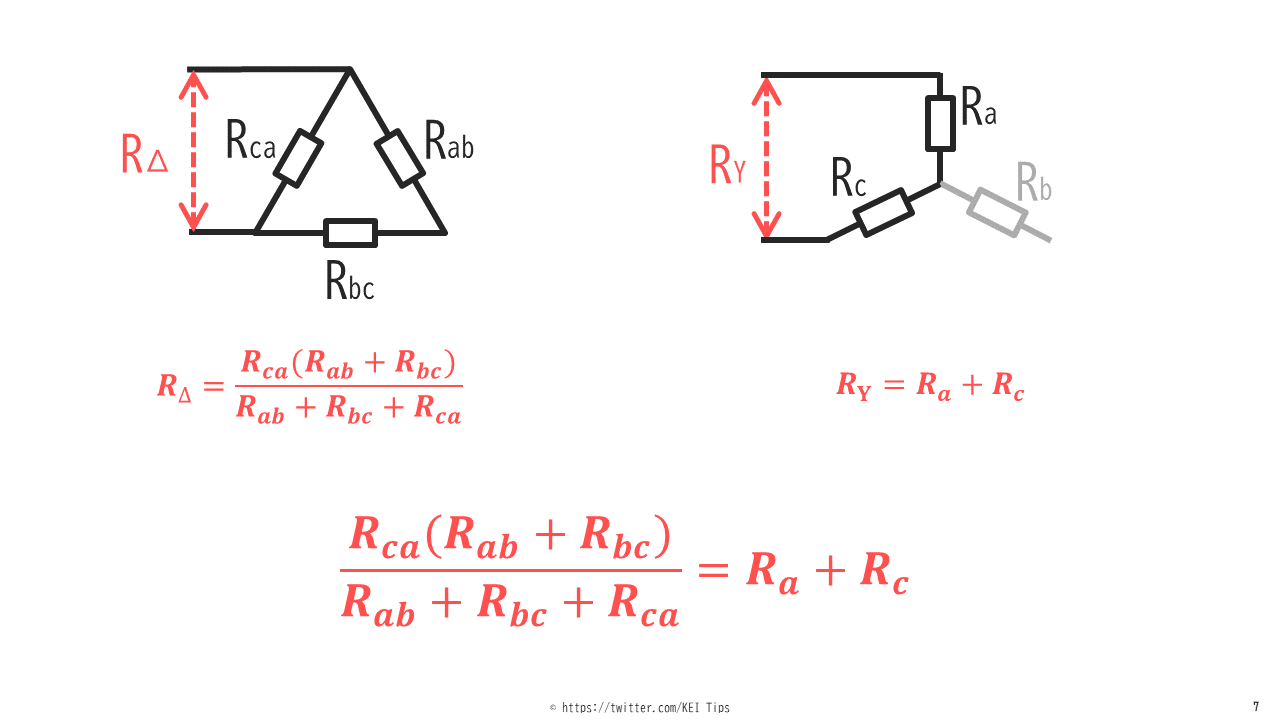
同じように他の2線間においても式を立てると、計3つの式が立てられます。
この3つの式を連立方程式として解くと冒頭に書いたΔ→Y変換、Y→Δ変換の公式が導けます。
(単純に求めていくだけなので計算は省きます)
おわりに
本サイトでは電気に関してこのような初学者でも分かりやすい解説を行っています。
もしこれを解説してほしい！という要望や質問がありましたらお問い合わせかXのDMでご連絡いただければと思います。
コメント