電験3種 各科目の解説
力率とは何かを文系にもわかりやすく解説

交流回路の電力を求める式は以下です。
$$\Large{P=VIcosθ}$$
この式のPは電力、Vは電圧、Iは電流、そしてcosθは力率といいます。この力率は交流回路の電力を計算するときに、電圧と電流の位相差を補正する値です。
といわれてもよくわかりませんよね。次から順を追ってわかりやすく解説していきます。
位相差がなければ力率を考えなくていい
そもそもの話、位相差がなければ力率を考える必要はありません。位相差がないとは図1のような状態です。
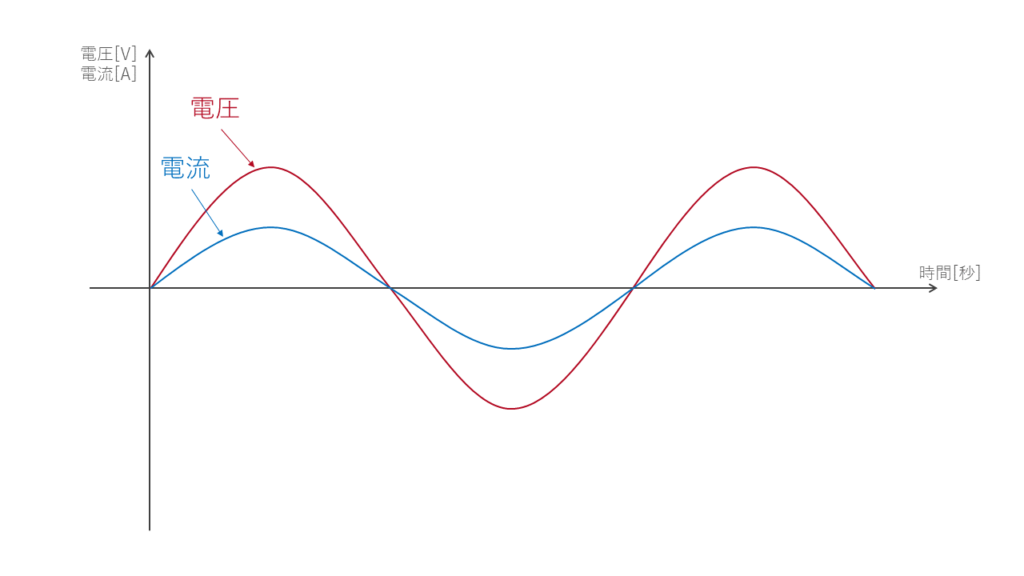
交流の電圧と電流は図1のような波形で表されます。図の横軸は時間です。
つまり位相差がないとは電圧と電流の時間的なずれがないということです。
位相差は電圧と電流の時間的なずれのこと
反対に位相差がある場合は図2のようになります。
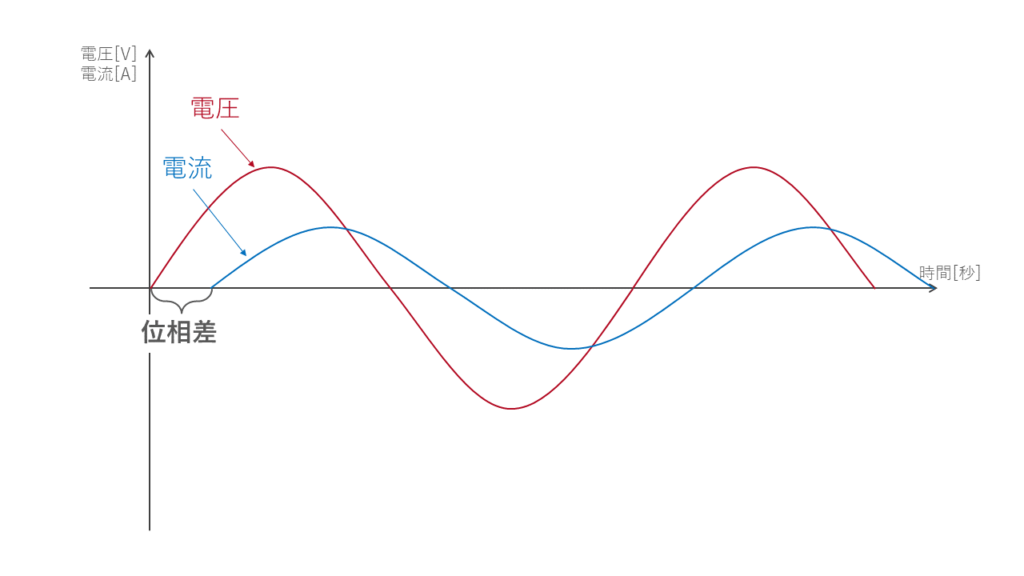
横軸の右にいくほど未来を表しているので、図2では電圧よりも電流が遅れてやってくるといえます。
これを電流の位相が遅れているといいます。そしてどれくらい遅れているかが位相差です。
ちなみに図3のように電流が進んでいるときの、進み度合いも位相差といいます。ただし通常は電流が遅れるケースがほとんどです。理由はありますが、難しいのでここでは説明を省きます。
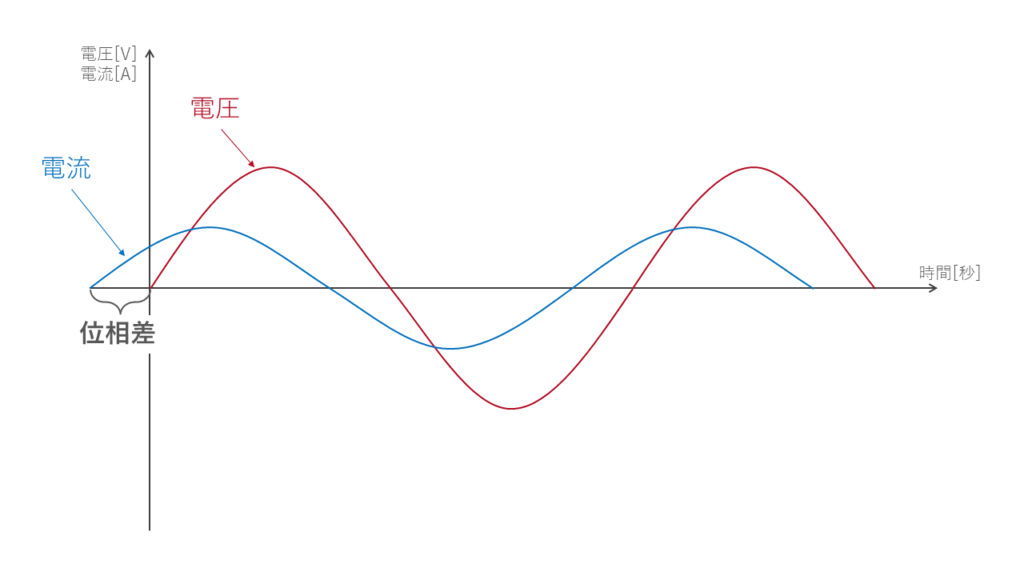
ちなみに位相差についてもっと理解したい方は↓のページで詳しく解説しています。

交流の100V、電流の1Aは実効値のこと
少し話が変わりまして、交流で100V(ボルト)、1A(アンペア)といえばそれは実効値のことです。どういうことか、図4の電流の波形で説明します。
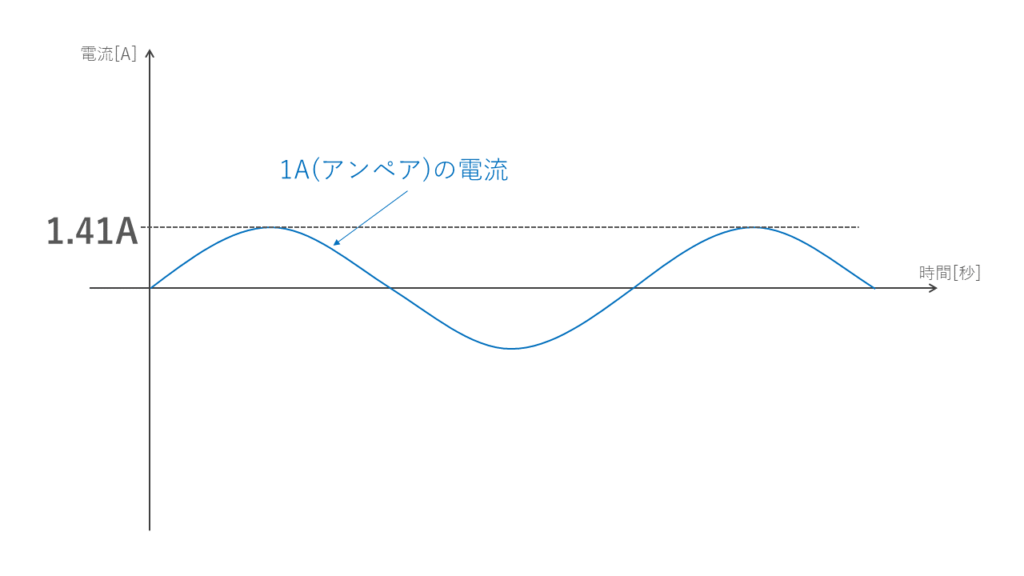
図4は1Aの交流電流です。がしかし、波形の一番大きい部分は1.41Aです。実効値は波形を直流に直したら何Aになるかを表しています。
交流電力は電圧の実効値と電流の実効値の掛け算で求めます。
交流電力はその瞬間の電圧×電流の合計である
交流電力は実効値同士の掛け算といいましたが、別の方法でも求められます。別の方法とは、その瞬間の電圧と電流をかけて1周期分を足し合わせる方法です。これを図5で説明します。
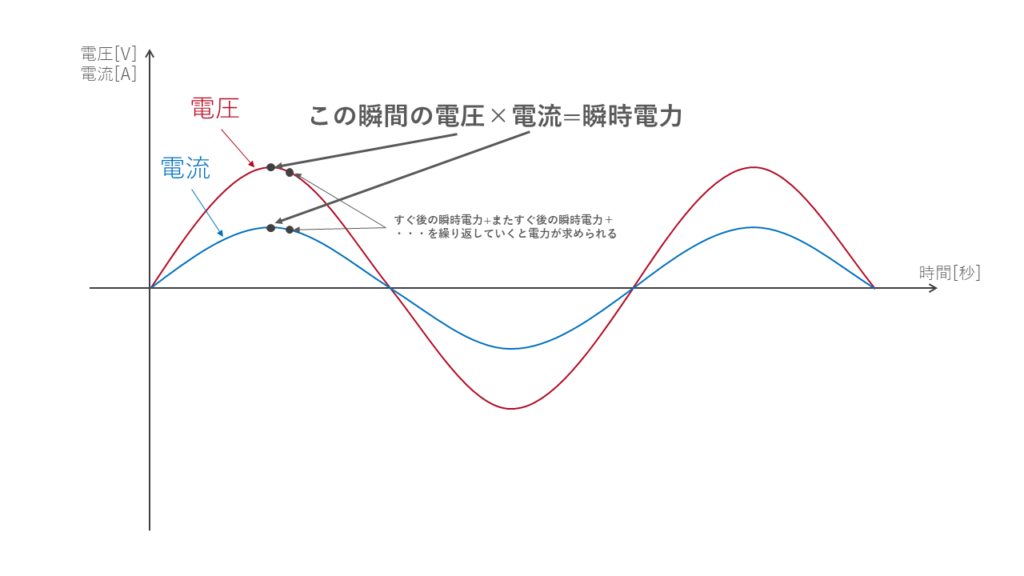
その瞬間の電圧と電流とは図5で示した部分で、この電圧と電流の積(掛け算の結果)は瞬時電力といいます。
そしてこの0.1秒後の瞬時電力を求め、更にその0.1秒後の・・・を繰り返して足し合わせると電力が求められます。
※0.1秒後といいましたが、本当はもっと短い時間で計算する必要があります。このもっと短い時間で計算をするためには積分をする必要がありますが、難しいので省きます。
位相差があるときは、1Aの電流を1Aとして電力計算できない
実効値の話と瞬時電力がなんとなく分かったところで、位相差のない時と、位相差があるときの話に戻りましょう。
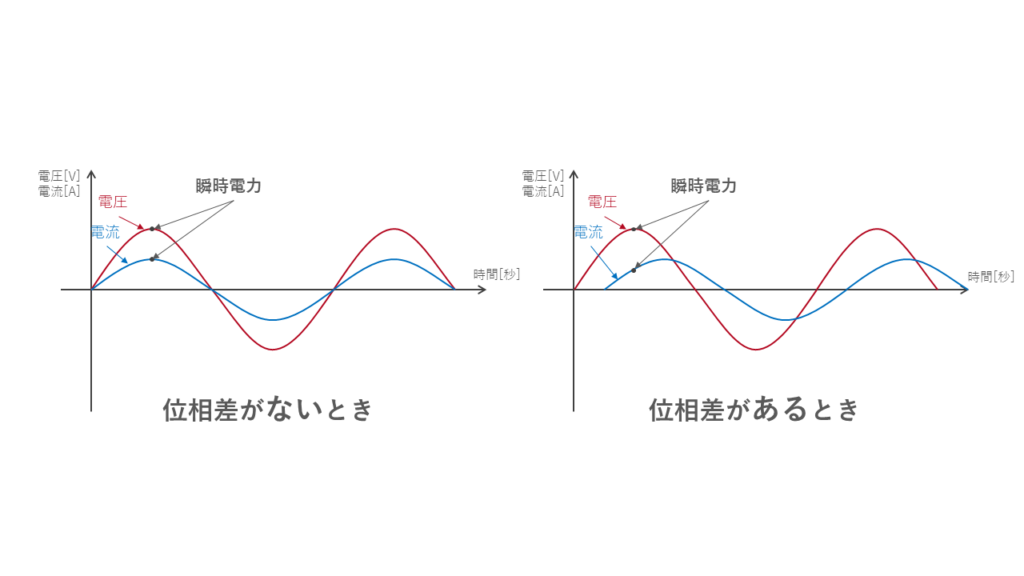
位相差がない時の瞬時電力と、位相差があるときの瞬時電力はパッと見た感じ明らかに違いますよね?
当然足し合わせても違う結果になります。なんとなく位相差があるときの方が足し合わせた電力が小さくなる気がしませんか?
実際小さくなります。
また位相差がないときは、電圧と電流の実効値同士の掛け算で電力が求められるのでした。
とすれば位相差があるときの電力は、電圧と電流の実効値同士の掛け算よりも小さい値になるような補正が必要です。
この補正が力率のことです。
時間のずれを角度のずれに変換する
じゃあどの程度補正すればいいのか?つまり力率はどのくらいの値になるのかはcosθを求めます。θは電圧と電流の位相差を角度で表したものです。
おいおいさっきまで位相差は時間のずれっていってたじゃない。と思うところですが、交流波形の時間的なずれは角度のずれに変換できます。
その変換式は以下です。
位相差(角度)=位相差(秒)×周波数×2×π
これで求めた位相差(角度)をθとしたときのcosθが力率になります。
またcosθは必ず1以下になります。このことからも、位相差があるときの電力が、位相差がないときの電力より大きくなることはないと分かります。
以上、力率の説明でした。
分かりやすさ重視のため難しい説明は省いています。気になる点があればコメント頂ければ補足しますのでお気軽にどうぞ。
















コメント