電験3種 各科目の解説
電気力線とは?本数と電界の関係をわかりやすく解説

電気力線とは電界の向きや大きさを分かりやすくするために引かれる仮想の線です。この電気力線の向きが電界の向きになり、本数が多いと電界も大きいことになります。
文字だけでは伝わりにくいと思うので、このページでは図も交えながら解説していきます。
電気力線とは何か?
まず電気力線とは何か?についてもう少し解説します。
電気力線とは電荷によって生じる電界を目で見えるように線で描いたものとイメージすると分かりやすいです。厳密にいえば少し違うのですが、ここではこのイメージでOKです。
また電気力線はあくまでわかりやすく計算をしたり、理解するために考えられた仮想の線であることを覚えておきましょう。
そのため次から電気力線の特徴を説明しますが、なぜそうなるんだ?と考えるのはあまり意味がありません。あくまで仮想の線ですのでそういうものだと覚えてしまいましょう。
では次から電気力線の特徴を解説していきます。
電気力線の特徴
特徴1:電気力線はプラスの電荷から出てマイナスの電荷に入る
電気力線はプラスの電荷から出てマイナスの電荷に入っていきます。例えば図1のように+Q[C]の電荷を帯びたとても小さい球体があるとします。この球体は点電荷と呼びます。図1は点電荷を真上からみたところです。
※[C]はクーロンと読み、電荷の大きさの単位です

この点電荷はプラスの電荷なので、図2のように電気力線が外に出ていきます。
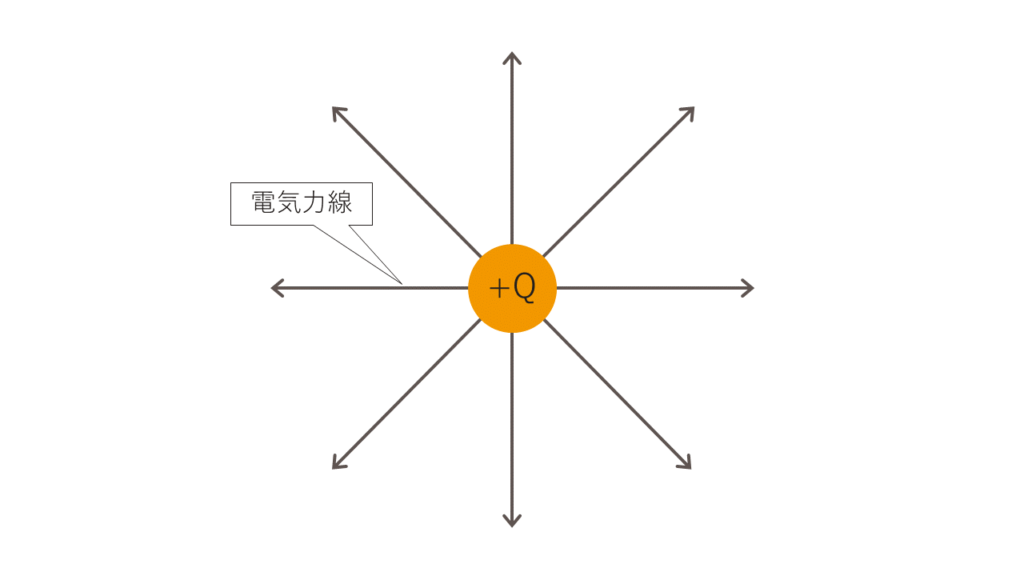
次にこのプラスの点電荷の隣に-Q[C]の電荷を帯びた点電荷を置きます。すると電気力線はプラスの電荷から出てマイナスの電荷へ入っていくので、図3のようになります。

特徴2:電気力線の本数は電荷の大きさと誘電率によって決まる
ある電荷から出る電気力線の本数は電荷の大きさと、電荷がある空間の誘電率で決まります。
電荷の大きさをQ[C]、誘電率の大きさをεとすると電気力線の本数は\(\displaystyle \frac{Q}{ε} \)で求められます。

特徴3:ある場所の1m2あたりに通る電気力線の本数が電界の強さになる
ある場所の1m2あたりに通っている電気力線の本数が、その場所の電界の強さになります。言い換えると、ある点での電気力線の密度が電界の強さになるということです。
ある場所1m2とは例えば図4に描いた四角のようなイメージです。図4の四角を1m2とすれば、ここを通る電気力線の本数がこの場所の電界の強さになります。

またついでに点電荷からr[m]離れた場所の電界の強さを考えてみましょう。
点電荷は電荷を帯びたとても小さい球体と考えます。また点電荷からは周囲に均等に電気力線が出ていくと考えることができます。なぜなら球体全体が均等に電荷を帯びているからです。
点電荷の大きさをQ[C]として、点電荷がある場所の誘電率をεとします。すると特徴2で書いたように、点電荷からでる電気力線の本数は\(\displaystyle \frac{Q}{ε} \)となります。これは点電荷から出る全ての電気力線の本数です。
よって図5のように放射状に\(\displaystyle \frac{Q}{ε} \)本の電気力線が点電荷からでていきます。

ここで図6のように点電荷を中心とした半径r[m]の球体を考えます。この球体の面を通る電気力線の本数は\(\displaystyle \frac{Q}{ε} \)です。
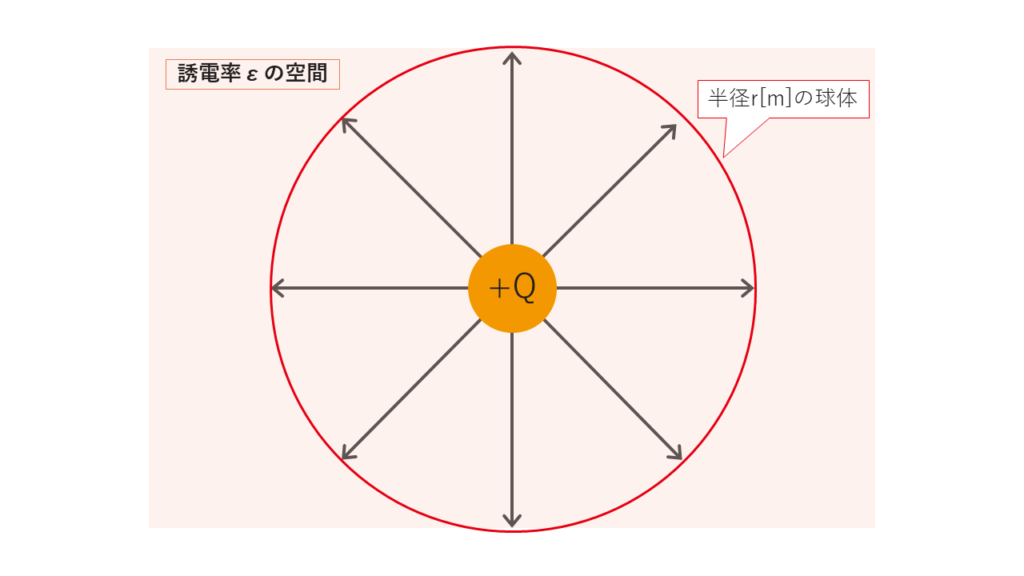
また球体の表面積は、球の面積の公式から4πr2となります。
これらを踏まえて、点電荷からr[m]離れた場所の電界を求めてみましょう。
電界はある場所1m2を通る電気力線の本数でした。そのため点電荷からr[m]離れた場所の電界は、点電荷からr[m]離れた場所1m2を通る電気力線の本数を、球体の表面積で割った値になります。
それを表したのが図7です。

これは電界の公式と同じになります。
結果的に公式が導入できました。公式を丸暗記するよりも、考え方を知っておくと捻られた問題が出題されても応えられるようになります。
特徴4:電気力線同士は反発するので、重なったり交わったりしない
電気力線同士は反発する特徴があります。そのため電気力線同士で重なったり交わることはありません。
電気力線同士は反発するから交わらないと覚えておきましょう。
特徴5:電気力線は途中で枝分かれしない
電気力線は途中で枝分かれをしません。1本の電気力線はずっと1本です。
例題を解いてみる
電気力線の特徴がわかったところで、試しに電験の問題を解いてみましょう。
まずは例題1からです。
例題1を解く
電界の状態を仮想的な線で表したものを電気力線という。この電気力線に関する記述として誤っているものを次の(1)~(5)のうちから一つ選べ。
(1)同じ向きの電気力線同士は反発し合う。
(2)電気力線は負の電荷から出て、正の電荷へ入る。
(3)電気力線は途中で分岐したり、他の電気力線と交差したりしない。
(4)任意の点における電気力線の密度は、その点の電界の強さを表す。
(5)任意の点における電界の向きは、電気力線の接線の向きと一致する。
このなかで(1)、(3)、(4)、(5)は今までみてきた電気力線の特徴から正しいと言えます。
しかし(2)に関しては電気力線はプラスの電荷から出てマイナスの電荷に入る特徴があるので逆です。
従って正解は(2)になります。
例題2を解く
続いて例題2を解いてみます。
4本の十分に長い導体円柱①~④が互いに平行に保持されている。①~④は等しい直径を持ち、図の紙面を貫く方向に単位長さあたりの電気量+Q[C/m]又はーQ[C/m]で均一に帯電している。ただしQ>0とし、①の帯電電荷は正電荷とする。円柱の中心軸と垂直な面内の電気力線の様子を図に示す。ただし電気力線の向きは示していない。このとき①~④が帯びている単位長さあたりの電気量の組み合わせとして正しいものを次の(1)~(5)のうちから一つ選べ。

まず問題文を読むと、①の電荷は正電荷と書いてあります。そのため①からは電気力線が出ていくことになります。
また問題の図をみると、①から出ていった電気力線は③と④の電荷へ入っていっています。電気力線はプラス出てマイナスに入るので、③と④は負の電荷と分かります。
そしてまた図をみると②と③の間も電気力線が走っています。③は負の電荷と分かっていますから、これは②の電荷から③の電荷へ電気力線が通っていると分かります。よって②の電荷は正電荷です。
これを満たす選択肢は(2)です。よって正解は(2)となります。
おわりに
本サイトでは電気に関してこのような初学者でも分かりやすい解説を行っています。
もしこれを解説してほしい!という要望や質問がありましたらお問い合わせかXのDMでご連絡いただければと思います。

















コメント