スカラー、ベクトル、フェーザの違いと基礎をわかりやすく解説

また電気の世界では、ベクトルをフェーザと呼んで計算などに使います。
ベクトルとフェーザは大体同じですが、全く同じかというと、そうではありません。これもまた分かりにくい部分です。

そこでページではそんな悩みを解消するため、以下について具体的に解説します。

• ベクトルとはなにか？スカラーとの違い
• フェーザとは何か
• フェーザ図の書き方
• フェーザを使う理由

スカラーとは？

ベクトルを理解するにはスカラーとの違いを理解するとわかりやすいです。
スカラーとは大きさだけの値です。例えば図1のような線上を歩くケースを考えてみましょう。

10m進み、更に5m進んだら最初の点から何m進んだことになるでしょうか？
これは当然10+5＝15mになります。

では今度は最初の位置から10m進んで5m戻ったら？
これも簡単で図2のように最初の位置からは10-5=5m進んだことになります。

このようにスカラーは大きさだけを含む値です。そのためプラス・マイナスの足し算や引き算だけで計算ができます。

ベクトルとは？

一方でベクトルとは「大きさと方向を持つ値」です。

先ほどのスカラーの説明では線上を歩くケースで考えました。ここではもう一本線を足して上下を移動できる人で考えましょう。

つまり図3のようにです。

では試しに右に10m、上に10m進むとします。
最初の位置から進んだ距離は何mになるでしょうか？
図4のように10+10=20m・・・ではありません。

図5のように最初の位置からは\(\sqrt{10^2+10^2}＝14.1m\)進んだことになります。

単純な足し算では計算できないことがわかるでしょうか？
これがベクトルは方向を持つ値といわれる理由です。

つまり「右に10m」と「上に10m」は大きさは同じですが方向が違うので異なる値として扱う必要があります。
そのため単純な足し算ができません。

このようにベクトルとは大きさと方向の2つの要素を持つ値です。

スカラーは一次元、ベクトルは二次元である

そして今までの説明で分かるのがスカラーは一次元の値であること。そしてベクトルは二次元の値であることです。

簡単に言うと一次元は線、二次元は平面です。

数学では二次元は図6のように横方向をx軸、上下方向をy軸として表現することが多いです。

なので先ほどの横に10m,上に10mはそれぞれ

$$\vec{x}=10,\vec{y}=10$$

と書きます。

そして最終的に移動した点は

$$\vec{x}+\vec{y}$$

と書きます。これをベクトルの合成といいます。
以上がベクトルの解説でした。続いてフェーザの話に移ります。

フェーザとは？ベクトルとの違い

フェーザはベクトルを電気の世界で使いやすくしたものです。

ベクトルとの違いは\(\vec{x}\)を実数、\(\vec{y}\)を虚数で表すことです。

つまりベクトルでは図7のように\(\vec{x}+\vec{y}\)と書いていたものをフェーザでは\(x+iy\)と書きます。(iは虚数単位)

複素数や虚数単位が分からない！という方は↓の記事で解説しているのでご参照ください。

ここでは以下3点を理解しておけばとりあえずOKです。

• iは2乗すると-1になる値
• 実数はいつも我々が使う値
• 虚数はiとセットで表される2乗するとマイナスになる値(例えばi3なら2乗すると-9になる)

フェーザ図を理解する

フェーザはベクトルと同じように平面上の点を表すことができます。

ただし前述のようにフェーザはベクトルのxを実数に、yを虚数にしたものですので図8のようになります。
(ちなみに実数の部分は実部、虚数の部分は虚部と呼ぶことが多いです。以降は実部、虚部と呼んでいきます。)

では実部が10、虚部は10のフェーザを例に考えてみましょう。
式にすると10+i10です。図で表すと図9のようになります。

フェーザで表すメリット

交流電圧や電流はこのフェーザで表すことが多いです。この理由は位相差のある電流や電圧の計算が楽になるからです。

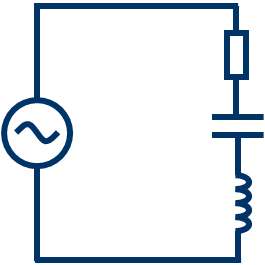
例えばコンデンサがあると位相が90°進む。もしくはコイル(インダクタ)があると位相が90°遅れる。と聞いたことがないでしょうか？

この90°のずれを計算するのにもフェーザは役立ちます。

フェーザにおいて90°遅れるは虚数単位iをかけることで表現できます。

例としてフェーザで表された10+i5を例に考えてみましょう。

これをフェーザ図で表すと図10です。

では10+i5にiをかけます。すると-5+i10になります。

これをフェーザ図にすると図11です。

このようにiをかけることで元のフェーザから90°遅れたフェーザにすることができます。

反対に90°進みの場合はどうでしょう？これは-iをかければOKです。-iをかけると図12になります。

元のフェーザから90°進んでいることがわかります。

このようにフェーザ(複素数)で電圧や電流を表現すると位相の遅れや進みの計算が楽になります。
これがフェーザを使うメリットです。

解説は以上になります。複素数については↓の記事で別途解説していますのでよろしければご覧ください。