交流回路の計算で使う複素数の基礎となぜ複素数を使うのかを解説

交流回路では電流や電圧、電力などを求めるために複素数を使います。複素数とは
〇+j〇で表される数のことです。
複素数を理解できると交流回路の計算がぐっと楽になります。このページでは↓の目次の内容をポイントに解説をしていきます。

複素数の基礎

まずは複素数の基礎を確認していきましょう。

複素数は実数+虚数で表される数

複素数は実数+虚数で表される数のことです。〇をある数字とすれば、実数+虚数は〇+j〇で表されます。

jは虚数単位といいます。これは2乗すると-1になる数です。高校の数学でも習ったはずですが、その時は虚数単位はjではなくiを使っていたかと思います。

電気の世界では電流をiで表すので混同しないようにjを使うことになっています。

実数はいつも使っている数

では実数とは何でしょうか？これは難しく考える必要はありません。いつも使っている数のことです。具体的には1,2,3・・・や-1,-2,-3・・・、この他に小数や分数も実数です。

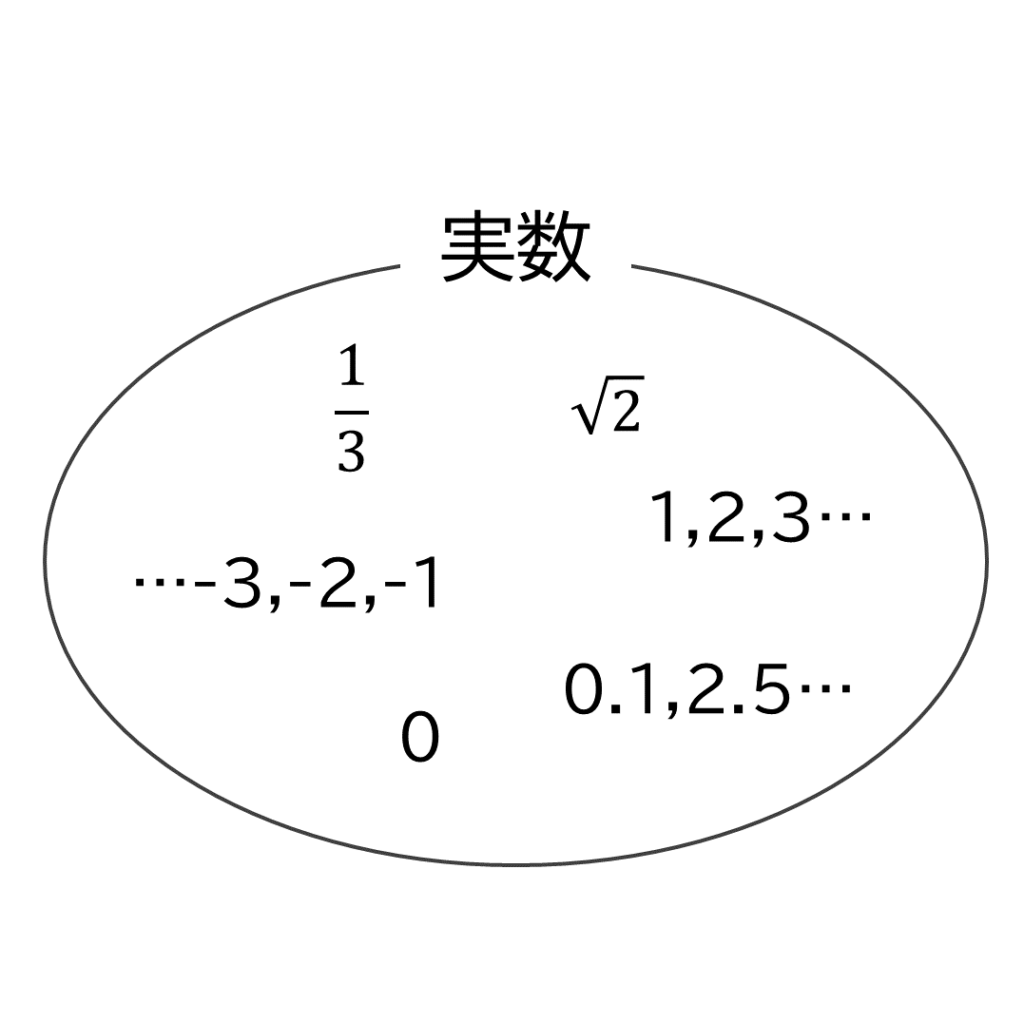
虚数は2乗するとマイナスになる数

対して虚数は2乗するとマイナスになる数です。でもこんな数現実的にはありません。
なぜならプラス×プラス＝プラス、マイナス×マイナス＝プラスと2乗すればどの数もプラスになるからです。

ですから本来は存在しない数なのですが、数学を考えるのに人が無理やり作った数が虚数です。これはなぜ？と考えるのは止めて、そういうものだと覚えてしまいましょう。

なぜ交流回路の計算に複素数を使うのか?

ここからはなぜ電気の交流回路を計算するのに、複素数を使うのかを解説していきます。

複素数は平面上の点で表せるから

複素数を使うメリットは、数を平面上の点で表せることです。どういうことか？まずは実数のみの場合を考えてみましょう。

実数は線上の点としてしか表せない

実数のみだと図2のように、線上の点でしか表すことができません。

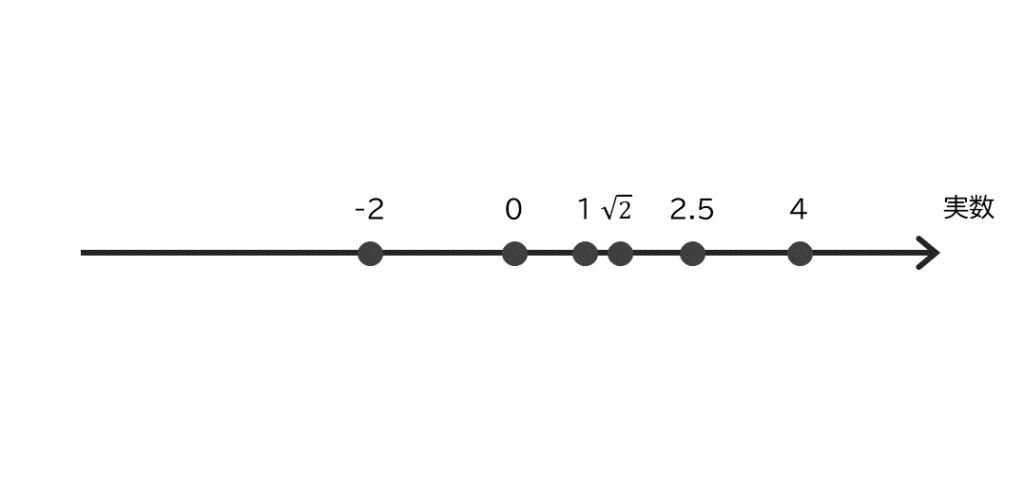
プラスだろうとマイナスだろうと、小数でも分数でも1直線の線上の点になります。

複素数は平面上の点で表せる

では実数に虚数を足して複素数にしてみます。虚数は実数とは異なる次元になります。簡単にいうと「実数が横線上の点であれば、虚数は縦線上の点」ということです。

つまり複素数は図3のような横軸を実数、縦軸を虚数とした平面上の点で表せることになります。

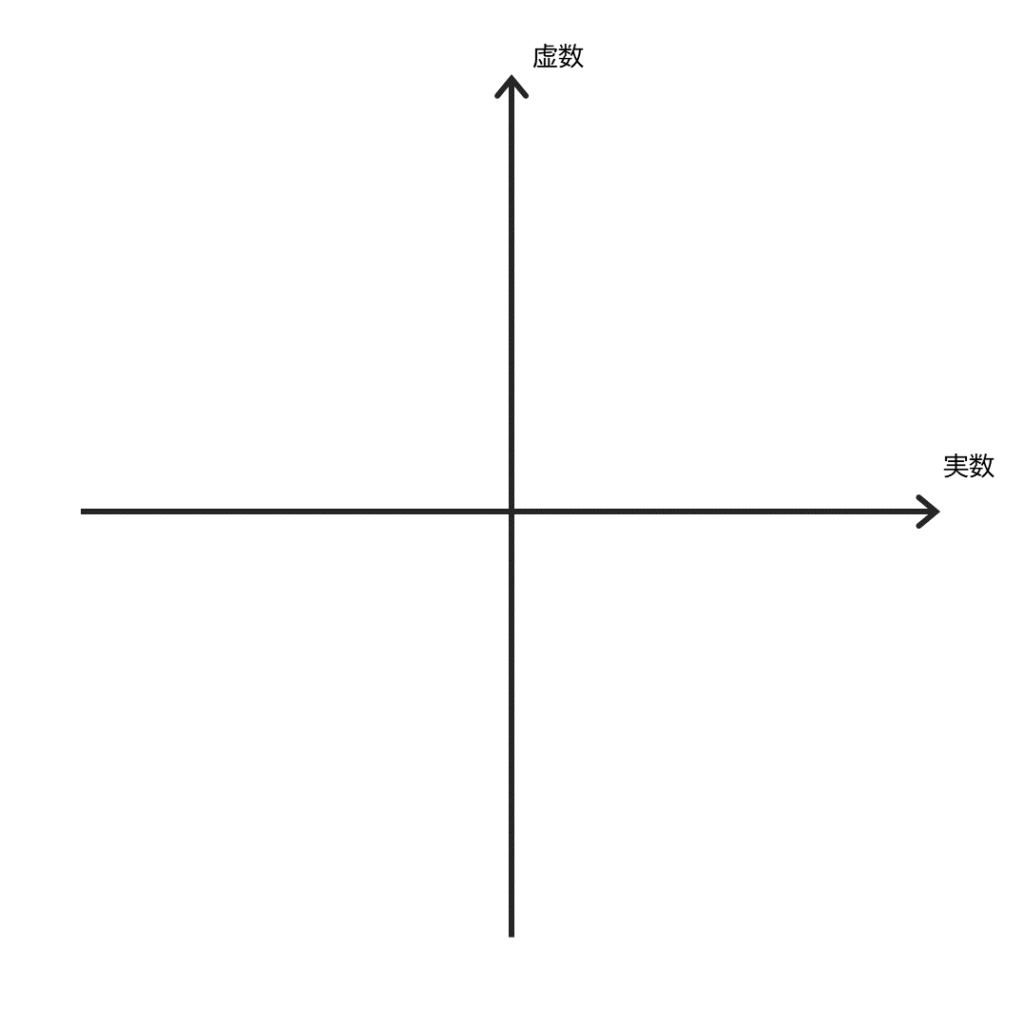
少し難しいので具体的な数値を入れて考えてみます。数値を平面上の点で表したのが図4です。

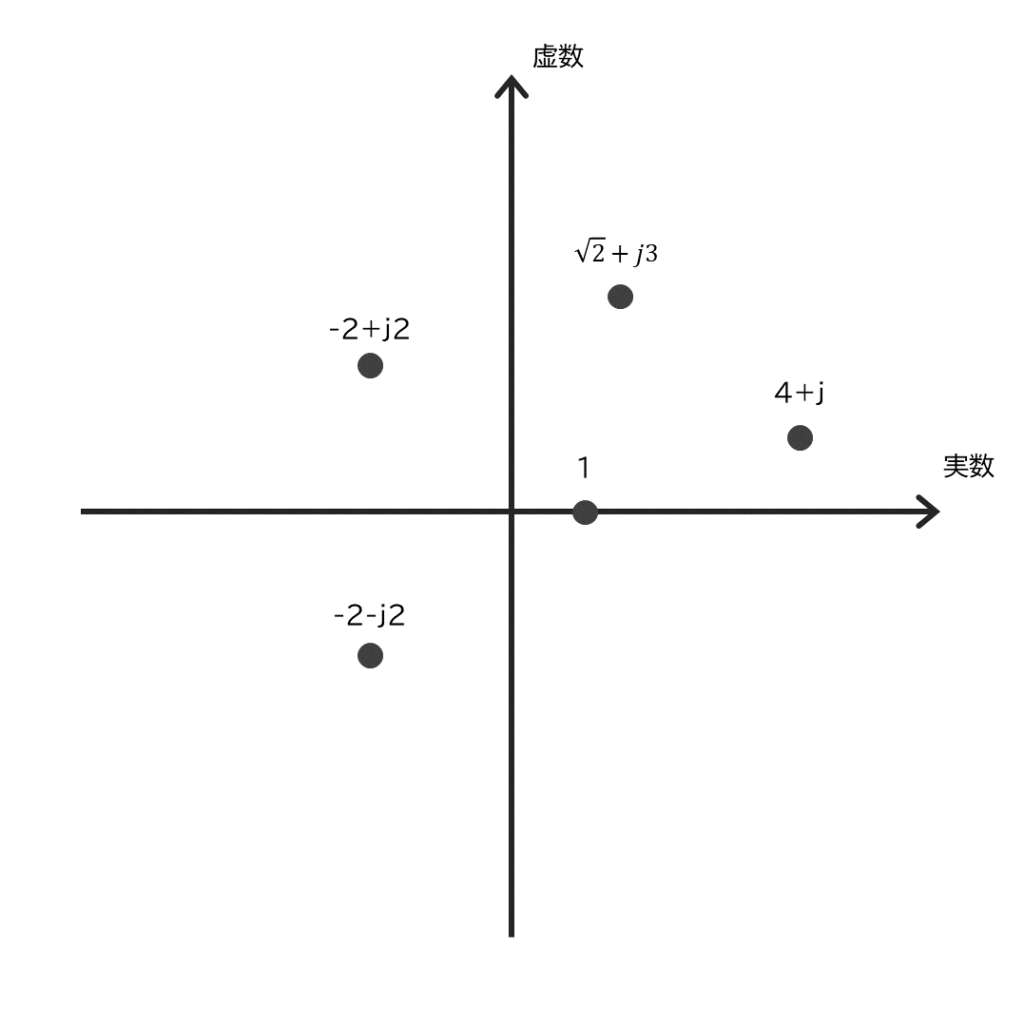
確かに複素数なら平面上の点で表すことができています。

複素数を使えば電圧や電流波形をベクトルで描ける

複素数は平面上の点で表せるのが分かったところでメリットを考えてみましょう。メリットは電圧や電流を複素数で表せばベクトルで表現できることです。

実は波形は円で表すことができます。それが分かるのが図5です。図5のように、波形上の点を投影していくと円を描くことが分かります。

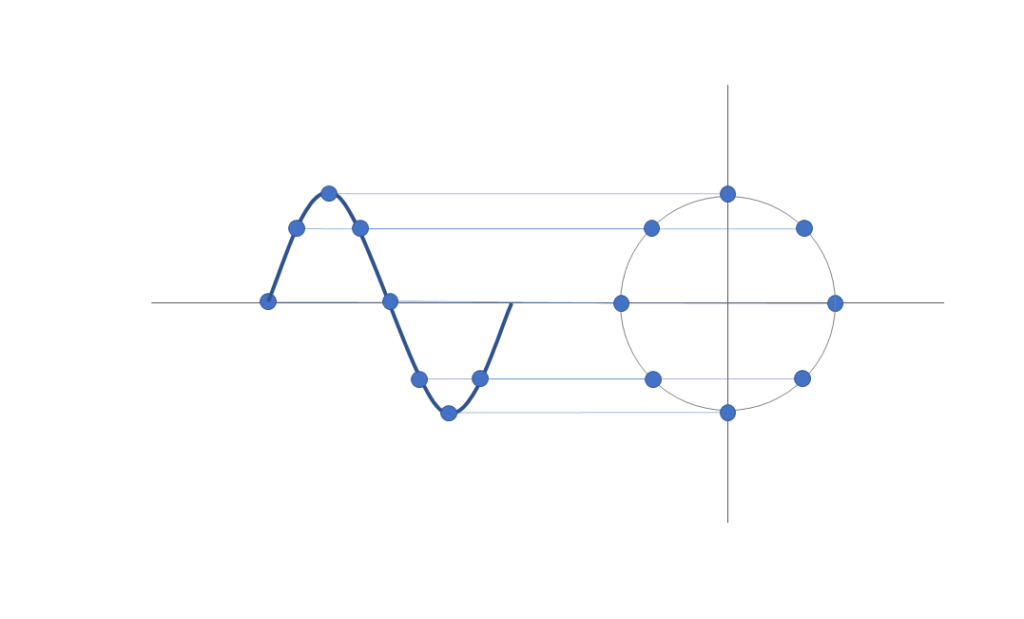
円上のある点は平面上にある点でもあるので複素数で表せます。

また図6のように0と円上の点を結ぶ矢印が波形を表すベクトルになります。

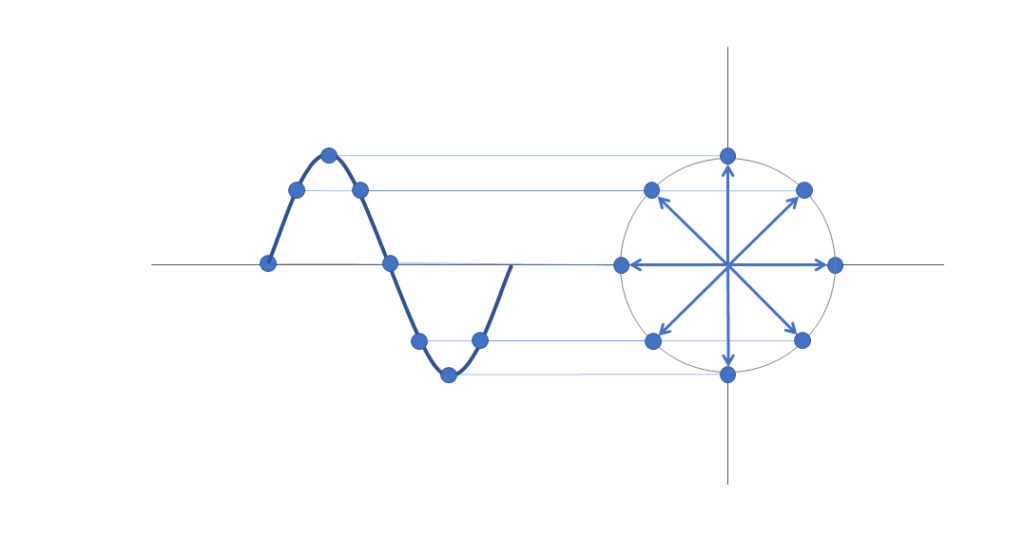
ベクトルで描ければ位相差を含めた計算が楽だから

ベクトルで表すと2つ以上の波形の位相差が分かりやすくなります。なぜなら位相差を角度で表せるからです。

図7は位相のずれた電圧と電流の波形です。

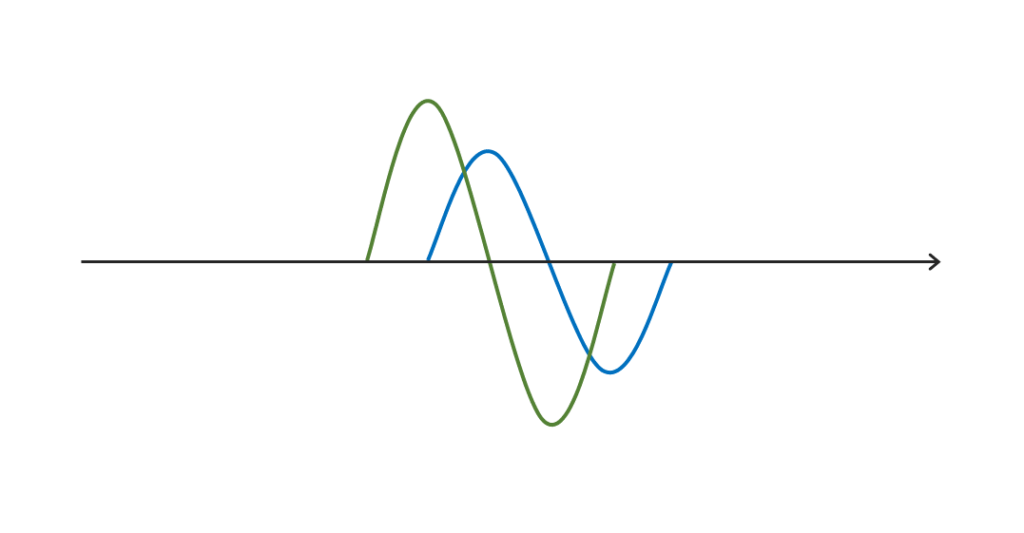
これをベクトルで表すと図8のようになります。二つのベクトルの角度が位相差になります。

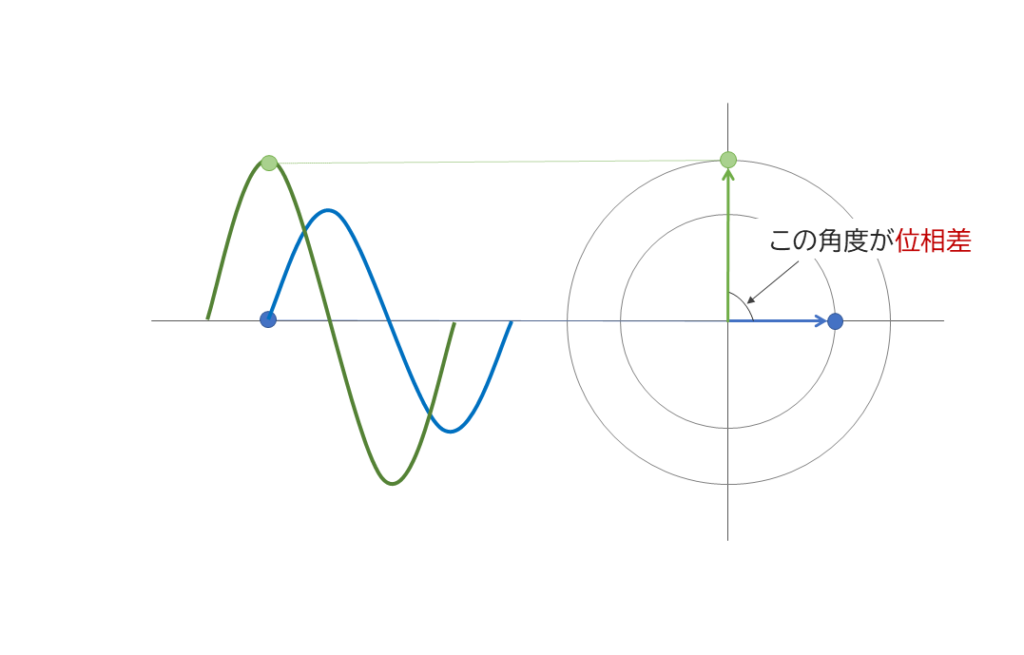
電力などの計算をする際は力率をかける必要があります。力率はcosθですがθが角度であると扱いやすくなるのです。

このようなメリットがあるので交流回路の計算では電流や電圧を複素数で表現します。