【電験三種理論】０から勉強する人に向けて交流回路の計算方法を解説します

交流回路の計算は直流回路の計算に比べて理解が難しくないでしょうか？

直流だと抵抗に電流を掛ければ電圧になり、電流と電圧の掛け算で電力が求められるので比較的理解がしやすいと思います。

一方、交流回路だと位相やインピーダンス、複素数などが出てきて計算もややこしくなります。この辺を理解するのはなかなか大変ですし、加えて計算自体も難しくなってきます。

そこでこの記事では交流回路の理解や計算につまずいている方に向けて、分かりやすい表現で交流回路について解説します。

ちなみに交流回路について勉強すると、聞き慣れない用語が出てきます。用語についてはこちらの記事でざっと説明しているので、先に読むと理解の助けになるかもしれません。

例題

交流回路の計算方法について勉強するにあたって、まずひとつ例題を考えてみます。

下の図の様な回路で回路に流れる電流iは何[A]になるでしょうか？

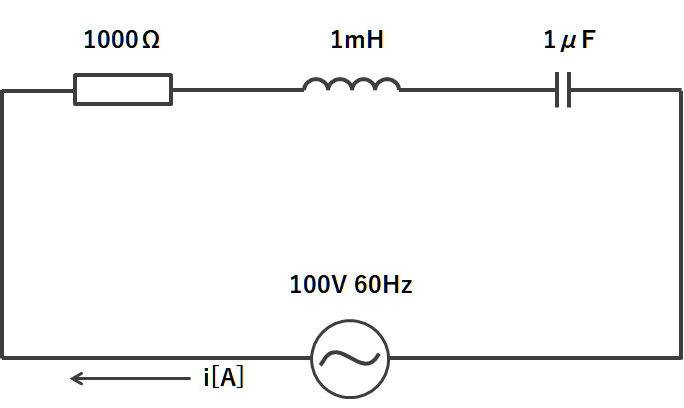
直流回路では電流を求めるにはオームの法則から$$I=\frac{V}{R}$$の式で電流が求められます。

交流回路でも同じ様にオームの法則が使えます。

しかし交流回路では抵抗の代わりにインピーダンスを使って計算しなくてはなりません。

交流回路のインピーダンスとは？

このインピーダンスとは、交流回路の抵抗分の様なものです。

リアクタンスとは？

交流回路では直流回路とは違い、回路のコイルやコンデンサも回路の抵抗分として考える必要があります。

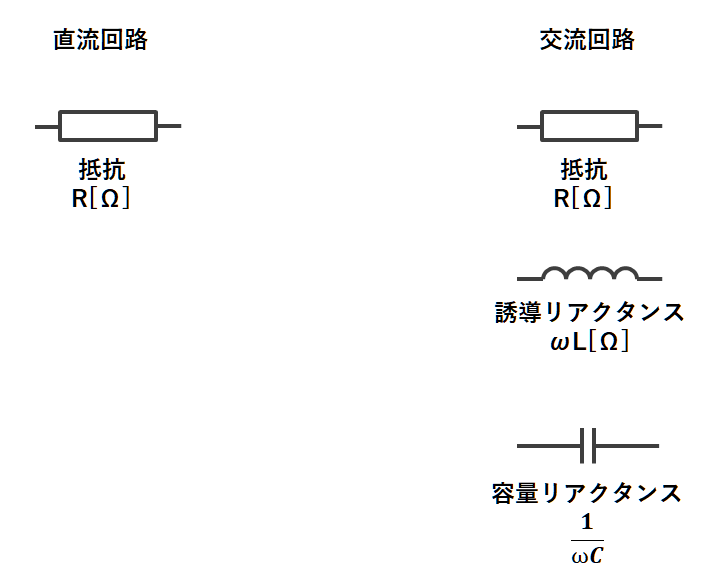
コンデンサによる抵抗分を容量リアクタンスと言い、コイルによる抵抗分を誘導リアクタンスと言います。

容量リアクタンスと誘導リアクタンスはコンデンサのキャパシタンスをC、コイルのインダクタンスをL、交流電圧の角周波数をωとして、以下の式で求められます。

単位は抵抗と同じ[Ω]です。

$$容量リアクタンス=\frac{1}{ωC}[Ω]$$

$$誘導リアクタンス=ωL[Ω]$$

リアクタンスと抵抗の和がインピーダンス

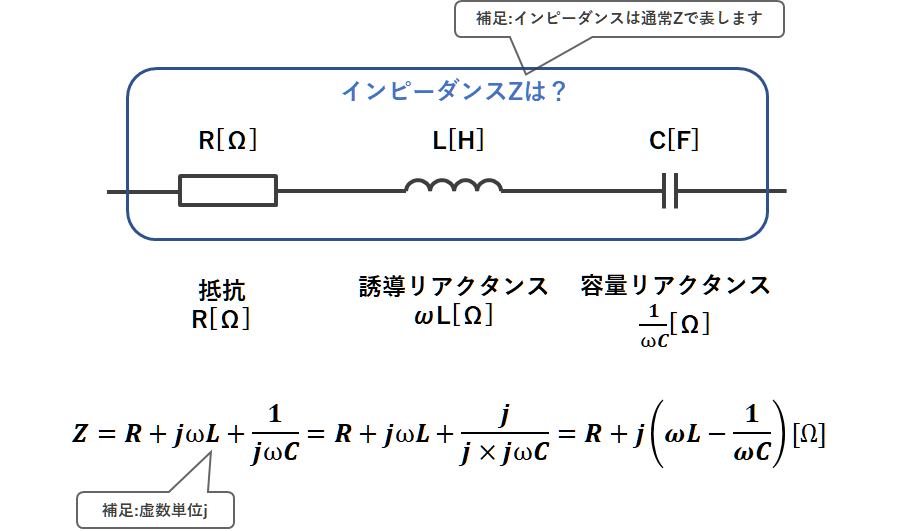
そしてこの２つのリアクタンスと抵抗Rの和がインピーダンスとなります。しかし和を求める時に注意が必要なポイントがあります。

抵抗Rとリアクタンスは単純に足し算ができません！

理由は抵抗は実数、リアクタンスは虚数として扱う必要があるからです。

そのためインピーダンスを求める際は、虚数単位jをωLとωCの前につけて、複素数として計算します。

複素数についてはこちら↓で解説しています。複素数がよく分からない方は読んでみてください。

電流を計算してみる

以上のことを理解したうえで、初めに出した回路に流れる電流を求めてみましょう。

まず誘導リアクタンスを求めます。

電源の周波数は60Hz、コイルのインダクタンスは1mHなので、$$誘導リアクタンス=jωL=j2πfL=j2π×60k×1×10^-3=j0.377[Ω]$$

次に容量リアクタンスは$$容量リアクタンス=\frac{1}{jωC}=\frac{1}{j2πfC}=\frac{1}{j2π×60×1×10^-6}=-j2654[Ω]$$となります。

これらと抵抗を足して回路のインピーダンスを求めると、$$インピーダンス=抵抗+誘導リアクタンス+容量リアクタンス=1000+j0.377-j2654=1000-j2653[Ω]$$

電流は$$電流=\frac{電圧}{回路のインピーダンス}=\frac{100}{1000-j2653}$$となります。

また電流の大きさを求める場合は$$電流の大きさ=\frac{電圧の大きさ}{インピーダンスの大きさ}$$の式で求められます。

つまり$$電流の大きさ=\frac{100}{\sqrt{1000^2+2653^2}}=0.035[A]$$となります。